Oscillation forcée d'un système "masse-ressort"

Considérons un système masse-ressort (voyez figure). Ce système mécanique est un exemple classique d'un système d'oscillation avec un degré de liberté. Le comportement de ce système est bien étudié et peut être décrit par des fonctions trigonométriques élémentaires qui sont pris en compte dans les manuels classiques physiques et mécaniques.

Dans notre cas, la force verticale harmonique est appliquée à la masse et le mouvement de la masse est autorisé à être seulement le long de l'axe Z (vertical). La force varie avec le temps par la loi harmonique:

F(t)=F0sin(ωft),

où  F0 est égal à 10 N.

ωf= 2π ff ,

où les gammes de fréquences ff de 5Hz à 30Hz.

Notre objectif est de trouver des amplitudes d'oscillation de la masse en utilisant les fréquences spécifiées.

Laissez-nous utiliser les données initiales suivantes: le diamètre moyen de la ressort est  D = 30 mm, la longueur du ressort est H = 100 mm,la section transversale du fil est un carré avec un côté d = 3 mm,  le nombre de spires N ressort est 6. Paramètres d'un poids sont ci-après: le diamètre DW= 40 mm, hauteur H=35 mm, la masse mW= 0.34306 kg.

Paramètres de la matière du ressort et le poids: le module d'élasticité E=2.1E+011Pa, coefficient de Poisson ν=0.28, densité ρ=7800kg/m3, module de cisaillement G=8.203E+010Pa, coefficient d'amortissement est égale à 2% relativement l'amortissement critique.

Classique analytique résolution

Amplitude des oscillations forcées harmoniques pour le système à un degré de liberté est décrite selon l'expression suivante

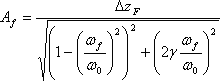                       (1)

où ΔzF est un déplacement sous l'action de forces statiques, qui est égale à l'amplitude de la force d'entraînement harmonique, ωf = 2*π*ff , ω0 = 2*π*f0- fréquence cyclique de la force et de la fréquence propre relativement; γ=c/ccr=0.02 - relatif coefficient d'amortissement. Fréquence d'oscillation libre du poids avec le ressort, qui sont considérés comme un système à un degré de liberté, est déterminée comme la célèbre expression suivante:

                                       (2)

où g est l'accélération en chute libre, m/s2; Δz est le déplacement de la masse statique en raison de l'action gravité. Déplacement statique est définie comme:

                               (3)

Le résultat de la résolution d'équation (3) donne un déplacement statique de la masse à cause de l'action de gravité Δzg=0.451 mm.

Donc, La résolution de l'analyse de l'équation (2) donne une valeur proche de la fréquence de système considéré avec un degré de liberté: f0 = 23.457 Hz.
Le déplacement de l'extrémité libre du ressort sous charge statique peut être calculée par la formule suivante:

,
où F est une force axiale.

Donc, déformation statique sous charge statique ΔzF = 1.342 mm. Si la résonance se produit (i.e. ff = f0), l'amplitude de vibration est égale à Af=ΔzF/2γ = 33.55 mm.

Solution numérique

Réglons cette étude par paquet AutoFEM analyse. L'extrémité supérieure du ressort est complètement fixé. Déplacements de la masse le long de l'axe X et l'axe Y sont interdites.

Le déplacement statique du système sous le poids est Δz*g = 0.428 mm (le résultat "Déplacement OZ" de l'étude "Static Analysis (gravity)").
Première fréquence propre est égale à f(1)c =23.594 Hz (le résultat "Mode 01 (23.594 Hz)" de l'étude "Frequency Analysis").
Le déplacement de l'extrémité libre du ressort sous charge statique est égale à Δz*F = 1.288 mm (le résultat "Déplacement OZ" de l'étude "Static Analysis (force)"). Que les rapports de l'amortissement de Rayleigh ont les valeurs suivantes: α= 0.02, β= 2.6891E-004. Ces valeurs correspondent à 2% de la résistance critique.

Le coefficient d'amortissement γ peut être définie par la formule suivante:

L'amplitude de la résonance vibratoire a la valeur suivante:  A*f=32.19 mm . Que l'on compare les résultats du calcul:

Tableau 1. Paramètres du maillage éléments finis

Tableau 2.  Les résultats.

 

 

 

*Les résultats des tests numériques dépendent du maillage éléments finis et peuvent différer légèrement de celles indiquées dans le tableau.

 

En savoir plus sur AutoFEM Oscillations Analysis

Retour au sommaire

autofem.com