Vibrations d'un système "ressort-masse" à cause de la fondation oscillant

Considérons le système masse-ressort. Le ressort est fixé sur un support vibrant, vibrations qui sont des harmoniques. L'amplitude d'oscillation est égale à 1.34192762 mm.

Laissez-nous utiliser les données initiales suivantes: le diamètre moyen de la ressort est  D = 30 mm, la longueur du ressort est H = 100 mm,la section transversale du fil est un carré avec un côté d = 3 mm,  le nombre de spires N ressort est 6. Paramètres d'un poids sont ci-après: le diamètre DW= 40 mm, hauteur H=35 mm, la masse mW= 0.34306 kg.

Paramètres de la matière du ressort et le poids: le module d'élasticité E=2.1E+011Pa, coefficient de Poisson ν=0.28, densité ρ=7800kg/m3, module de cisaillement G=8.203E+010Pa, coefficient d'amortissement est égale à 2% relativement l'amortissement critique.

Notre objectif est de trouver des amplitudes d'oscillation de la masse, en utilisant les fréquences, qui va de 5Hz à 30Hz. Les rapports de l'amortissement de Rayleigh ont les valeurs suivantes: α= 0.02, β= 2.6891E-004. Ces valeurs correspondent à 2% de la résistance critique.

Amplitude des oscillations forcées harmoniques pour le système à un degré de liberté est décrite selon l'expression suivante

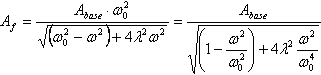,                (1)
où Abase est une amplitude d'oscillation de la base,ω est la fréquence angulaire des oscillations de la base, ω0 est la fréquence angulaire naturelle des oscillations du système, λ est le coefficient d'amortissement.

Notons l'expression λ/ω0= γ, puis la formule (1) passe au-dessus:

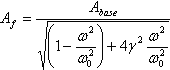,                                        (2)
où le coefficient γ est calculé par la formule suivante:

.                                                (3)

Les coefficients α, β sont le coefficient d'amortissement de masse et le coefficient d'amortissement de rigidité, respectivement.

La raideur du ressort est calculée par la formule:
.                                                        (4)

Donc, le ressort a une raideur à la suite:
.

Ensuite, la fréquence angulaire naturelle  est
,
et la fréquence propre est
.

Laissez-nous calculer les amplitudes A f par la formule (2) pour les fréquences f1=5Hz, f2=10Hz, f3=15Hz, f4=20Hz, f5=f0, f6=25Hz, f7=30Hz and γ=0.02.

Donc, A1f= 1.4057 mm, A2f= 1.6396 mm, A3f= 2.2682 mm, A4f=4.8773 mm, A5f= 33.8482 mm, A6f= 9.4208 mm, A7f= 2.1041 mm.

Réglons cette étude par l'Analyse AutoFEM.

L'extrémité supérieure du ressort oscille avec une amplitude étant égale à 1.34192762 mm. Déplacements de la masse le long de l'axe X et l'axe Y sont interdites.

Après avoir effectué les calculs de la AutoFEM analyse les résultats suivants sont obtenus:

Tableau 1. Paramètres du maillage éléments finis

Tableau 2. The result “Amplitude”

 

 

 

*Les résultats des tests numériques dépendent du maillage éléments finis et peuvent différer légèrement de celles indiquées dans le tableau.

 

En savoir plus sur AutoFEM Oscillations Analysis

Retour au sommaire

autofem.com