 |
 |
 |
 |
 |
 |
AutoFEM Analysis Grande déflexion d'une plaque circulaire sous une charge uniformément répartie |  |
|
|
|
|
|
|
AutoFEM Analysis Grande déflexion d'une plaque circulaire sous une charge uniformément répartie | |
Grande déflexion d'une plaque circulaire sous une charge uniformément répartie
Considérons une plaque circulaire avec le rayon a et de l'épaisseur h. La plaque est fixée long de sa contour et soumises à une charge uniformément répartie, avec l'intensité q (voyez figure).
|
Le modèle éléments finis d'une plaque circulaire sous une charge uniformément répartie (grands déplacements) |
Laissez-nous utiliser les données initiales suivantes:le rayon de la plaque est a = 0.25 m, l'épaisseur de la plaque est h = 0.005 m, l'intensité de charge est q = 1E+05 Pa.
Propriétés du matériau sont E=2.1E+011 et ν= 0.28.
Servons-nous de la formule analytique suivante pour calculer les déplacements du centre de la plaque:
,
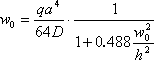où
est la rigidité de flexion de la plaque.
Pour résoudre cette équation pour w0, on obtient la valeur de la déviation maximale, ce qui est attendu dans le centre de la plaque: w0= 2.3258E-003 m.
Après avoir effectué les calculs (en prenant en compte la non-linéarité) par le AutoFEM analyse les résultats obtenus sont les suivants:
Tableau 1. Paramètres du maillage éléments finis
Type d'élément fini |
Nombre de nœuds |
Nombre d'éléments finis |
tétraèdre quadratique |
3000 |
8720 |
Tableau 2. Résultat “Déplacement, magnitude”
Solution numérique |
Solution analytique |
Erreur δ =100%*|w0*- w0|/| w0 | |
2.2938E-003 |
2.3258E-003 |
1.38 |
|
* Les résultats des tests numériques dépendent du maillage éléments finis et peuvent différer légèrement de celles indiquées dans les tableaux.
En savoir plus sur AutoFEM Static Analysis
