Contraintes et les déformations d'une plaque orthotrope sous une contrainte biaxiale

 

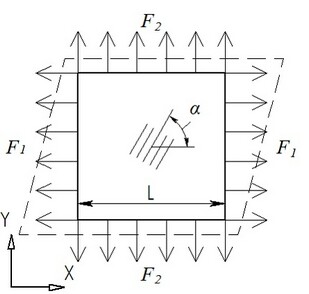
Considérons une plaque carrée fabriqué avec des matériaux orthotropes, avec la longueur de la côté L, qui est chargé avec les forces F1 et F2, appliquée aux bords de la plaque. La largeur de la plaque est h.
Nous avons besoin de définir les contraintes et les déformations de la plaque. Supposons que: F1=20,000 N, F2=10,000 N, L=0.1 m, et h=0.005 m.
Paramètres du matériau sont les suivantes: Modules d'élasticité sont Е1=5.59·1010 Pa, Е2=1.373·1010 Pa, Е3=1.373·1010 Pa, modules de cisaillement sont G12=5.59·109 Pa,  G23=4.904·109 Pa,  G31=5.59·109 Pa, et les coefficients de Poisson sont ν12=0.277, ν23=0.4, ν31=0.068. L'angle d'élévation de l'axe de symétrie principal est α=45°.

Tout d'abord, au centre de la plaque, nous créons un système de coordonnées utilisateur (nommé «Ortho») à l'aide d'AutoCAD commande "UCS".  Puis, nous l'importer dans AutoFEM analyse. Ce système de coordonnées définit les axes d'anisotropie du matériau de notre plaque. Pour les régler, il faut utiliser de commande "Propriétés d'Anisotropie".
Pour stabiliser le modèle, cochez la case «Stabiliser le modèle non fixée" (page "Résolution" des propriétés de l'étude).
Appliquer une charge normale avec F1 grandeur à une paire de facettes latérales parallèles, et F2 charge normale, à l'autre paire.

Laissez-nous effectuer un calcul statique de la plaque à l'aide de la commande "Résoudre". Nous allons obtenir des résultats sous forme de déformations et de contraintes.

 

 

Valeur moyenne des déformations ОХ εx*=3.177·10-4, des déformations ОY εy*=2.107·10-3,
Contraintes principales sont les suivantes: σ1*=4,000·107 Pa, σ2*=2,000·107 Pa.

La solution analytique des contraintes principales prend la forme suivante:

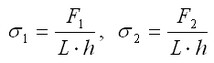
σ1=20000/0.005/0.01=4·107 Pa, σ2=10000/0.005/0.01=2·107 Pa.

Déformations selon les axes OX, OY sont calculées en utilisant les formules suivantes:

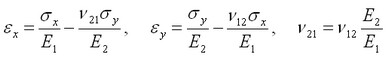
ν21=0.277·1.373·1010/5.59·1010=0.06804
εx=3.0·107/5.59·1010 – 0.06804·3.0·107/1.373·1010=3.88·10-4;
εy=3.0·107/1.373·1010 – 0.277·3.0·107/5.59·1010=2.036·10-3;

Après calculs menée avec l'aide de AutoFEM Analyse par la méthode directe, nous avons obtenu les résultats suivants:

Tableau 1

Tableau 2

Tableau 3

 

 

*Les résultats des tests numériques dépendent du maillage éléments finis et peuvent différer légèrement de celles indiquées dans le tableau.

 

En savoir plus sur AutoFEM Static Analysis

Retour au sommaire

autofem.com