Contatto tra una barra cilindrica e un anello

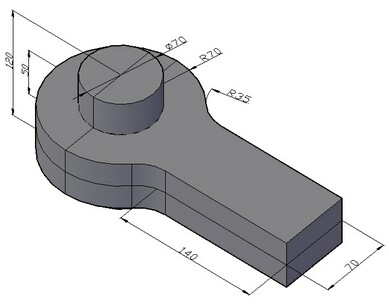
Consideriamo il contatto tra la barra cilindrica infilita in un anello (si veda figura seguente). Si suppone che le parti non sono legate insieme e ciascuna parte può muoversi liberamente entro l'altra senza attrito. Una forza di intensità P che direzionata lungo la normale dell'anello è applicata all'estremità libera dell'anello.

Usiamo i seguenti dati iniziali: P = 1E+005 N, d = 0.07 m è il diametro dell'asse cilindrica, H = 0.12 m è la lunghezza dell'asse, R = 0.07m è il raggio esterno dell'anello dell'occhio, h=0.05 m è lo spessore dell'anello, b = 0.07 m è la larghezza della cinghia dell'anello, L= 0.14 m è la lunghezza della cinghia dell'anello, r = 0.035 m il raggio di transizione dell'anello.
Le proprietà del materiale sono: il modulo di Young E = 2.1E+011 Pa e il coefficiente di Poisson ν = 0.28.
La sollecitazione lungo la normale nella sezione di nastro dell'anello può essere calcolata utilizzando la seguente formula semiempirica:

 

σ = k*P / h*(2*R - d), dove k  è il fattore di concentrazione della tensione (k = 3.6).

σ = 1.0286E+008 Pa.

 
Dopo aver effettuato i calcoli dal AutoFEM Analysis, sono stati ottenuti questi risultati:

La solleccitazione lungo la normale dell'anello σX ha valori che variano da 0.8E+008 Pa a 0.99E+008 Pa.
Paragoniamo σX con σ:

Tabella 1. Parametri della maglia ad elementi finiti

Tabella 2. Risultato "Sollecitazione normale OX”*

 

 

* I risultati dei test numerici dipendono dalla maglia ad elementi finiti e possono differire leggermente da quelli indicati nella tabella.

 

Approfondire riguardo ad AutoFEM Analisi Statica

 

 

 

Torna ai contenuti

autofem.com