 |
AutoFEM Analysis Axial Vibration Frequency and Transverse Vibration Frequency of the Beam with the Weight (surface) | ||||||
 |
AutoFEM Analysis Axial Vibration Frequency and Transverse Vibration Frequency of the Beam with the Weight (surface) | ||||||
Frequenze di vibrazione assiale e trasversale di una trave sottoposta ad un carico concentrato
Consideriamo la trave a sbalzo, alla cui estremità destra vi è posizionato un peso.
|
La lunghezza della trave è L. Il fascio sezione trasversale è un rettangolo di larghezza b e altezza h. La massa del peso è M. La massa specifica del fascio è m.
m = ρ F,
dove F = b h, ρ è la densità del materiale del fascio.
|
Il modello ad elementi finiti con carichi e vincoli |
Sia L è pari a 0,5 m, b è pari a 0,02 m, h è pari a 0,05 m.
Le proprietà del materiale sono: il modulo di Young E = 2.1E + 011 Pа, coefficiente di Poisson ν=0.28, la densità ρ = 7800 kg / m3.
La massa del peso M è uguale a 2.m.L kg (i.e. 7.8 kg).
Soluzione analitica di questo problema è dato dalle seguenti formule:
a) la frequenza di vibrazione assiale
![]()
b) la frequenza di vibrazione trasversale
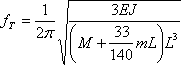 ,
,
![]() .
.
Perciò, fA = 1078.962 Hz , fT = 22.092 Hz.
Dopo aver effettuato il calcolo con l'aiuto di AutoFEM, i seguenti risultati sono stati ottenuti:
Tabella 1.Parametri della mesh ad elementi finiti
Tipo di Elemento Finito |
Numero di Nodi |
Numero di Elementi Finiti |
triangolo lineare |
165 |
256 |
Tabella 2. Resultato "Frequenza"*
Frequenza (soluzione numerica) f*, Hz |
Frequenza (soluzione analitica) f, Hz |
Errore δ = 100%*| fi* - fi| / | fi | |
22.269 |
22.092 |
0.80 |
1080.440 |
1078.962 |
0.14 |
|
|
*I risultati dei test numerici dipendono dagli elementi finiti della maglia e possono differire leggermente da quelli indicati nella tabella.
Aprrofondire riguardo ad AutoFEM Frequency Analysis