Analisi statica di un disco solido rotante di spessore uniforme

Consideriamo un disco di raggio R e spessore uniforme h (si veda figura).

Nell'analisi consideriamo solo 1/4 del disco applicando condizioni di simmetria ai bordi (nessuno spostamento nelle direzioni degli assi del sistema di coordinate locali,  il quale è  in posizione normale rispetto al piano di simmetria).
Il disco è sottoposto alla forza centrifuga F = ρω2R, dove ρ è la massa del volume unitario del disco (correlata al tipo di materiale), ω è la velocità angolare di rotazione.

Usiamo i seguenti dati: R 0.457, h 0.01 m, ω 300 rad/s.
Caratteristiche del materiale: modulo di Young E = 2.1E+011 Pa; coefficiente di Poisson ν = 0.28, densità della barra ρ = 7800 kg/m3 .
Per questo problema, lo spostamento u può essere determinato dalla formula:
,
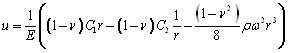dove le costanti C1 = (3+ν)ρω2R2 / 8, C2 = 0 sono determinati dalle condizioni al contorno.
Il massimo spostamento umax dovrebbe essere r = R, che è umax = (1-ν)ρω2R3/4E

Componenti di tensione σr , σθ  sono trovati come:

,

.
Queste sollecitazioni hanno il valore massimo al centro del disco dove:
σr =σθ = (3+ν)ρω2R2 / 8

Quindi, umax = 5.7430E-005 m, σr =σθ =σ = 6.0111E+007 Pa

Dopo aver effettuato il calcolo con l'aiuto di AutoFEM, sono stati ottenuti questi ottenuti:

Tabella 1. I parametri della maglia ad elementi finiti

Tabella 2. Risultato "Spostamento"*

Tabella 3. Risultato "Sollecitazione Equivalente"*

 

 

* I risultati dei test numerici dipendono dalla maglia ad elementi finiti e possono differire leggermente da quelli indicati nella tabella.

 

Approfondire riguardo ad AutoFEM Analisi Statica

 

 

Torna ai contenuti

autofem.com