Fonte di calore uniformemente distribuita di forma cilindrica posta all'interno di un disco

Si considera un problema di stato stazionario bidimensionale riguardante la distribuzione di temperatura ai bordi del disco al quale è applicata una fonte uniformemente  distribuita di forma cilindrica posta al centro del disco con un raggio rd=20 mm e potenza P  = 100 W. Alla periferia vi è mantenuta una temperatura costante di 273.15 oK.

Parametri del disco: disco di metallo di spessore d=5 mm, raggio R=100 mm e conduttività termica K=50 W/(m • oK) [lega di acciaio (SS)].

(si veda la figura).

La soluzione di questo problema nel quale la fonte di calore è considerata come uniformemente distribuita può essere ottenuta dalla soluzione del problema per una fonte di calore puntuale. Il sistema di coordinate coincide con il centro della superficie del disco. L'equazione differenziale che a seguire verrà risolta è quella riguardante il problema per una fonte di calore puntuale:

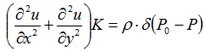
dove ρ è la densità della potenza distribuita. La soluzione di questa equazione è conosciuta e per il nostro caso: ρ = P/ (2π•rd•d) = P/S, dove S è l'area della superficie  del cilindro. Dalla presa in considerazione del tipo di distribuzione della potenza intorno all'anello del cilindro possiamo esprimere la temperatura come il totale della somma dato dalla potenza di tutti i punti applicati:

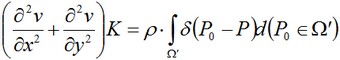
dove Ω è l'insieme dei punti sulla superficie del disco, Ω’ è l'insieme dei punti che giace all'interno della superficie del disco a sono disposti sull'anello della fonte di calore cilindrica. La soluzione di questa equazione ν è una combinazione lineare delle soluzioni puntuali ciascuna per ogni punto della fonte di calore:

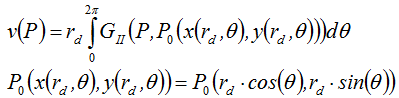
dove GII dè una funzione di Green per una potenza defiunita dalla formula , per una distribuzione sulla superficie . Dopo aver integrato ottteniamo: where GII – is a

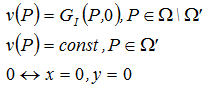
Quì GI è una funzione di Green per una potenza definita dalla formula ρ = P/S per una sorgente puntuale distribuita sui bordi. Questo implica che l'intensità della temperatura v coninciderà con la temperatura da un punto della sorgente (localizzato al centro del cerchio) per punti che giacciono fuori fuori rispetto all'anello su cui è distribuita la fonte di calore descritta. Nei punti interni, la temperatura prenderàil valore uguale a qualche costante. Notiamo che v è una funzione continua e che questo è dato dal fatto che levalore della costante interna è sempre conosciuta.

Compariamo la soluzione analitica con la soluzione ottenuta all'AutoFEM, di seguito i seguenti risultati sono stati ottenuti: Let us compare analytical solution with the solution obtained from AutoFEM. After carrying out calculation the following results are obtained:

Tabella 1. Parametri degli elementi finiti della maglia

Tabella 2. Resultato "Temperature"

 

Questa immagine rappresenta la distribzione di calore per una sorgente posizione lungo i bordi

Conclusioni:

Per il dato problema abbiamo ottenuto una realistica interpretazione del campo della temperatura. L'errore relativo della soluzione numerica comparata con la soluzione analitica non eccede lo 0.03% quando si usano gli elementi lineari ai bordi del disco.

In aggiunta, noi notiamo che la modellazione di un problema relativo a una fonte di calore non puntuale derivato da un problema relativo ad una fonte dicalore pun tuale è stato possibile in questo caso, questo non è sempre possibile, ma solo per certe sitiazioni geometriche che dipendono dalla simmetria.

 

 

* I risultati dei test numerici dipendono dalla maglia ad elementi finiti e possono differire leggermente da quelli indicati nella tabella.

 

Approfondire riguardo ad AutoFEM Analisi Termica

 

 

Torna ai contenuti

autofem.com