Oscillazione forzata di un sistema "molla-massa"

Consideriamo un sistema dato da una molla alla quale è appeso un grave di forma cilindrica. Questo sistema meccanico è un classico esempio di un sistema oscillante ad un grado di libertà. Il comportamento di questo sistema è ben studiato e può essere descritto da funzioni trigonometriche elementari che sono mostrate in manuali di fisica alla sezione meccanica classica.

Si trascuri le possibili perturbazioni (oscillazioni lungo X Y) e si consideri permessa solo l'oscillazione della molla in senso verticale lungo l'assa Z dovuta al grave. La forza F varia nel tempo con legge armonica:

F(t)=F0sin(ωft),

dove  F0 è uguale a 10 N.

ωf= 2π ff

e si sppone che la frequenze ff vari da 5Hz a 30Hz.

Il nostro scopo è di trovare le ampiezze di oscillazione del grave dovuto alla variazione di frequenza supposta.

Usiamo i seguenti dati iniziali:  D = 30 mm è il il diametro medio della molla, H = 100 mm è la lunghezza della molla, la sezione trasversale del filo presenta forma quadratica con un lato d = 3 mm, n = 6 è il numero delle spire. I parametri del grave sono i seguenti: DW= 40 mm è il diametro della superficie circolare, H=35 mm l'altezza, mW= 0.34306 kg la massa.

Parametri del materiale della molla e del grave: modulo di elasticità E=2.1E+011Pa, coefficiente di Poisson ν=0.28, densità ρ=7800kg/m3, modulo di taglio G=8.203E+010Pa, coefficiente di smorzamento è il 2 % rispettivamente allo smorzamento critico.

Classica soluzione analitica.

Ampiezza delle oscillazioni armoniche forzate per il sistema con un grado di libertà è descritto secondo la successiva espressione:

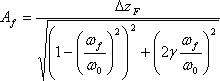                       (1)

dove ΔzF è la il delta di spostamento della molla sottopposta ad azione della forza di gravità del grave, ωf = 2*π*ff è la frequenza angolare di oscillazione alla frequenza ff,ω0 = 2*π*f0 è la frequenza angolare naturale per il sistema non smorzato detto di punto zero, 0; γ=c/ccr=0.02 è il coefficiente di smorzamento, che è rapporto dell'ammortizzazione reale sopra la quantità di ammortizzazione richiesta per raggiungere lo smorzamento critico. L'oscillatore "molla-massa" può essere considerato come un sistema ad un grado di libertà, e le sue frequenze possono essere determinate dalla seguente espressione:

                                       (2)

dove: g è l'accelerazione di gravità espressa in m/s2; Δz è lo spostamento statico della massa a causa di azione dell'accelerazione di gravità.

Lo spostamento statico è definito come:

                               (3)

dove m è la massa del grave in kg;  D è il diametro medio della molla in mm, n è il numero delle spire della molla, d è la lunghezza del filo in mm, G è modulo di taglio in Pa.

Il risultato della risoluzione di equazioni (3) dà lo spostamento statico del peso per azione della gravità

Δzg=0.451 mm.

Quindi, la risoluzione analitica dell'equazione (2) dà un valore di frequenza successiva al punto 0, per il sistema considerato con un solo grado di libertà f0 = 23.457 Hz.

Perciò l'ampiezza dello spostamento della estremità libera della molla sottoposto a carico statico può essere calcolato utilizzando la seguente formula:

dove F è una forza assiale in Newton.

ΔzF = 1.342 mm .

Se la risonanza si verifica (i.e. ff = f0), l'ampiezza vibrazionale Af uguale a:

Af=ΔzF/2γ = 33.55 mm.

Soluzione numerica

Si risolva questo studio con AutoFEM Analysis.

Lo spostamento statico del sistema sotto il peso proprio è Δz*g = 0.428 mm (il risultato "Spostamento OZ" dello studio "Static Analysis (gravity)").
La prima frequenza di vibrazione della molla sottoposta a carico statico è f(1)c =23.594 Hz (il risultato "Mode 01 (23.594 Hz)" dello studio "Frequency Analysis").
L'ampiezza dello spostamento dell'estremità libera della molla sottoposta a carico statico è uguale a Δz*F = 1.288 mm (il risultato "Spostamento OZ" dello studio "Static Analysis (force)").
Si Lasci che i coefficienti di smorzamento di Rayleigh abbiano i seguenti valori: α= 0.02, β= 2.6891E-004. Questi valori corrispondono al 2% della resistenza critica.
Il coefficiente di smorzamento γ può essere definito dalla seguente formula:

L'ampiezza di risonanza vibrazionale ha il seguente valore: A*f=32.19 mm .

Ora, si confronti i risultati dei calcoli:

Tabella 1. Parametri della maglia ad elementi finiti

Tabella 2. I Risultati

 

 

 

* I risultati dei test numerici dipendono dalla maglia ad elementi finiti e possono differire leggermente da quelli indicati nella tabella.

 

Approfondire riguardo ad AutoFEM Analisi Oscillazioni

 

 

 

Torna ai contenuti

autofem.com