 |
AutoFEM Analysis Gradiente di temperatura in una piastra isotropica a trasmissione di calore per convezione | ||||||
 |
AutoFEM Analysis Gradiente di temperatura in una piastra isotropica a trasmissione di calore per convezione | ||||||
Gradiente di temperatura in una piastra isotropica a trasmissione di calore per convezione
Si consideri una piastra metallica di dimensioni b x a=100x200 mm e di spessore D=5 mm con conduttività termica K=50 W/(m oK) [Lega metallica (SS)]. Mostreremo come il problema di stato stazionario può anche essere risolto per il caso in cui la temperatura sui bordi della piastra non è mantenuta costante (per modelli corretti la temperatura deve essere preventivamente conosciuta). Consideriamo due tipi di carichi: flusso di calore (uguale a zero su alcuni bordi) e trasferimento di calore per convezione. Sulla superficie del piatto (da entrambi i lati) noi descriviamo lo scambio di calore con l'ambiente esterno con un coefficiente di trasferimento di calore C=40 W/(m2 • oK) e la temperatura dell'ambiente esterno è uguale u0=283.15 oK. (si veda figura)
|
Consideriamo l'origine del sistema di coordinate posizionato ad un angolo della piastra, l'asse OY è direzionato sul lato lungo della piastra, e la convezione saraà allora applicata alla faccia y = b. Allora noi dedurremo che due su tre bordi, sui quali non vi è flusso di calore, corrispondono ai valori x=0 e x=a. Questo dice che la soluzione che noi otteniamo non deve dipendere dalle coordinata x. Soluzioni avranno la forma:
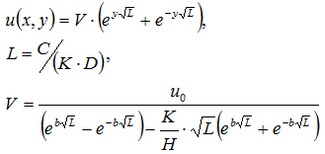
Qui di seguito vi mostriamo le linee isotermiche per la soluzione ottenuta utilizzando il software Maple.
La convezione è applicata per la coordinata Y = b.
|
|
Linee istomermiche per soluzioni ottenute con il programma Maple. La convenzione è applicata ai bordi y=b. Quando y=0 il flusso termico è zero |
I sensori di temperatura come visto in figura sono posizionati lungo y a 170; 180; 190; 200 mm. In questi punti metteremo a confronto la soluzione numerica ottenuta utilizzando Analysis AutoFEM con la soluzione analitica.
|
|
Il modello ad elementi finiti con applicate le condizioni al contorno |
Dopo aver effettuato i calcoli sono stati ottenuti i seguenti risultati:
Tabella 1. Parametri degli elementi finiti della maglia
Tipo di elemento finito |
Numero di nodi |
Numero di elemnti finiti |
tetraedro lineare |
462 |
1200 |
Tabella 2. Risultati "Temperature"
Coordinate y, mm |
Soluzione Numerica |
Soluziona Analitica |
Errore δ = 100%* |T* - T| / |T| |
170 |
273.2773 |
273.2783 |
3.55E-04 |
180 |
273.3029 |
273.3033 |
1.43E-04 |
190 |
273.3325 |
273.3332 |
2.67E-04 |
200 |
273.3669 |
273.3690 |
7.86E-04 |
|
Conclusions:
L'errore relativo della soluzione numerica comparata con la soluzione analitica non eccede lo 0.0008% per gli elementi in progressione lineare.
Il problema è stato risolto con il minimo costo computazionale.
* I risultati dei test numerici dipendono dalla maglia ad elementi finiti e possono differire leggermente da quelli indicati nella tabella.
Approfondire riguardo ad AutoFEM Analisi Termica