Gradiente termico in un disco isotropico

Consideriamo adesso il problema di un disco con fonti di calore distribuite sulla superficie. Consideriamo il flusso di calore prescritto su entrambi i lati. Intorno al disco lungo i bordi noi prescriveremo la temperatura costante.

Come nell'esempio noi consideriamo un disco sottile con la conduttività termica K=75 W/(m • oK) [Ferro duttile (SN)]. Il raggio del disco è R=100 mm e lo spessore D=5 mm. La valore della densità del flusso di calore è F=60 W/m2. La temperatura dei bordi intorno al disco e T=293.15 oK. (si veda figura)

L'equazione che deve essere risolta per una superficie di un disco ha la seguente forma:

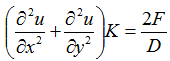
Al lato destro dell'equazione noi habbiamo la densità volumetrica della fonte di calore (equivalente alla densità di superficie per un problema a onde piane).

Condizioni limite:

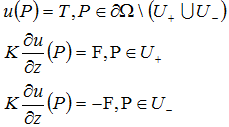
dove U-  e U+ sono rispettivamente il lato inferiore e superiore del piatto. La soluzione analitica può essere in termini della funzione della sorgente di calore G(P, P0).

Questa funzione è una soluzione dell'equazione di Laplace per solo lato destro (al lato destro noi abbiamo una funzione di Dirac) per un potere unitario.

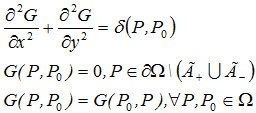
La soluzione dell'equazione di Poisson può essere espressa in term della funzione sorgente come

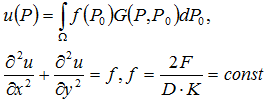
La soluzione analitica è stata calcolata con il sistema Maple 9.5 dal metodo di integrazione numerica _d01ajc (Integrazione di Gauss usando 10 punti e Croncord integration usando 21 punti). Noi abbiamo usato 6 cifre significative di accuratezza nella soluzione analitica per confrontare i risultati.

Consideriamo di aver localizzato i sensori della temperatura come mostrato in Figura e facciamo un disegno di loro a r =0; 20; 40; 60 mm. Nei dati punti noi confronteremo la numerica soluzione ottenuta usando l'Analisi Auto FEM con la soluzione analitica.

Dopo il calcolo i seguenti risultati sono stati ottenuti:

Tabella 1. Parametri degli elementi finiti della maglia

Tabella 2. Risultati "Temperature"

 

Conclusioni:

L'errore relativo della soluzione numerica comparata con la soluzione numerica non supera lo 0.0008% per gli elementi in progressione lineare.

Il problema è stato risolto quasi esattamente comparato con il minimo costo computazionale. è importante notare che un punto r=20 mm la soluzione con elementi lineari si è rivelato essere più accurato. Questo era realmente possibile perchè dalle proprietà di convergenza della soluzione nel metodo ad elementi finiti (convergenza nel senso della norma integrale e piccolo numero di punti /argomenti giocano un ruolo qui). Perciò, in generale è impossibile predirre l'aspetto e e la posizione di questi punti.

 

 

* I risultati dei test numerici dipendono dalla maglia ad elementi finiti e possono differire leggermente da quelli indicati nella tabella.

 

Approfondire riguardo ad AutoFEM Analisi Termica

 

 

Torna ai contenuti

autofem.com