Ridiazione di una piastra nell'ambiente esterno

Consideriamo adesso un problema di calcolo per uno stato stazionario di temperatura per un'infinita piastra che irradia l'ambiente esterno. Sui lati della piastra lungo la lunghezza, noi manteniamo una costante temperatura di T=500 oK (noi assumiamo che per questa temperatura l'effetto della radiazione per questa piastra sarà significante). La radiazione prenderà il posto della superficie della piastra su entrambi i lati della piastra con un ambiente esterno con una temperatura uguale a Text=293 oK. Adesso assumendo lo stato stazionario, noi determiniano il campo di temperatura sulla superficie della piastra a punti controllati che sono disegnati dai sensori (localizzati sull'asse OX).

Le caratteristiche del piatto: spessore d=5 mm; lunghezza l=100 mm;conduttività termica K=50 W/(m • oK); emissività α=1. Noi manteniamo il flusso di calore pari a zero lungo i bordi della lunghezza della piastra. (si veda figura)

 

Consideriamo l'equazione differenziale per questo problema. Dalla flusso termico di calore sui lati opposti della piastra è uguale a zero, il campo di temperatura cambierà solo lungo la lunghezza della piastra. Dalla selezione del sistema di coordinate così che l'asse OX è diretto lungo l'ampiezza della piastra e l'asse OY lungo la lunghezza, noi otterremo la soluzione che dipende solo dall'ampiezza della piastra. Noi posizioneremo l'origine, O, delle coordiante del sistema al centro della piastra. L'equazione allora prenderà la forma:

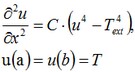
dove la costante C è determinata dalla presa in considerazione della lunghezza della piastra come:

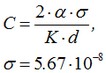
dove σ è la costante di Boltzmann.

La soluzione analitica per questo problema può essere trovato come una serie di Taylor. Esso può essere ottenuto numericamente nel sitema Maple 9.5. Noi consideremo il valore lungo la lunghezza solo nel punto medio, i.e., l'origine selezionata del sistema di coordinate, poiché la soluzione è una funzione pari (dal punto di vista fisico esso è ovvio perchè noi abbiamo uguale temperatura lungo i bordi e il materiale è isotropico. Nel centro noi avremo il punto di minimo perchè il coropo perde calore).

Consideriamo adesso di presentare la soluzione per il problema come una serie. Noi notiamo che  

poichè dal punto di vista fisico la piastra non potrebbe raffreddarsi ad una temperatura inferiore alla temperatura ambiente. Perciò, ∂u/∂x cresce in maniera monotona da -  a + ciò che significa che ha un singolo punto di intersezione con l'asse OX il quale sarà il punto di minimo della soluzione. Nella regione vicina di questo punto noi abbiamo espanso la soluzione in una serie:    

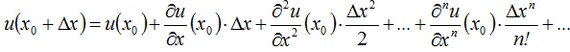
dal differenziamento della data equazione noi otterremo le espressioni per il più alto ordine delle derivate:

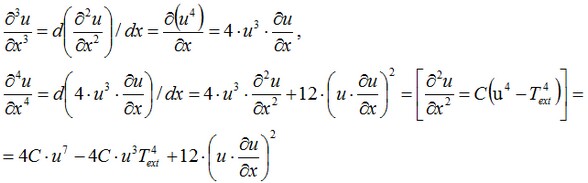
e così via. Esso è ovvio che tutte le derivate possono essere rappresentate nella forma di un polinomio F della funzione u e i valori delle sue derivate prime

Per tutte le derivate dispari, tutti i termini del polinomio F conterrà come un fattore delle derivata prima e perciò al punto di estremo noi abbiamo

Perciò la soluzione prenderà la forma:

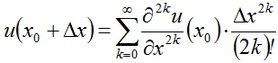
Esso è ovvio dalla simmetria delle condizioni limite che il punto x0 coincide con lo zero O selezionato dal sistema di coordiante.

Non c'è semplice soluzione analitica per poichè per ciascun passo del calcolo della somma della serie, noi abbiamo bisogno di immaganizzare tutti i coefficienti del polinomio F per valutare la derivata del prossimo step. Che è perchè noi abbiamo usato tradizionali viae di valutazione analitica delle derivate attraverso il sistema Maple 9.52*. Il valore di u in un punto x0 è stato ottenuto nella seguente via: noi selezioniamo parziali serie di Taylor al punto x0 +l/2 e eguagliamo loro al valore limite della temperatura T. LA soluzione di queste equazioni può essere trovata numericamente e, perciò, solo le reali radici positive erano di interesse. Come un risultato da noi ottenuto u(0) = 467.4671303.

Consideriamo i sensori della temperatura localizzati come mostrato in Figura a facciamo un grafico lungo Y = 0; 12.5; 25; 37.5 mm. Nei dati punti noi confronteremo la soluzione numerica ottenuta usando l'Analisi AutoFEM con la soluzione analitica:

 

Dopo aver effettuato i calcoli i seguenti risultati sono stati ottenuti:

 

Tabella 1. Parametri degli elementi finiti della maglia

Tabella 2. Resultati "Temperatura"

 

Conclusioni:

L'errore relativo della soluzione numerica comparato con la soluzione analitica è uguale allo 0.8% per i valori sull'asse della piastra. Notiamo che quando la maglia è rifinita, la convergenza della soluzione numerica alla soluzione analitica è lenta per problemi con radiazioni poichè il problema è non lineare.

Quando risolvendo un non lineare problema esso non importa quali elementi sono usati per calcoli: lineari o quadratici.

 

 

* I risultati dei test numerici dipendono dalla maglia ad elementi finiti e possono differire leggermente da quelli indicati nella tabella.

**  Il ciclo sui numeri dei termini della serie  sono stati performati differenziando e sostituendo con una potenza alla quarta la derivata seconda e ponendo zero le derivata prima nella finale espressione.

Approfondire riguardo ad AutoFEM Analisi Termica

.

 

 

Torna ai contenuti

autofem.com