 |
AutoFEM Analysis Deformazione massima di una piastra rotonda sopposta ad un carico uniformemente distribuito | ||||||
 |
AutoFEM Analysis Deformazione massima di una piastra rotonda sopposta ad un carico uniformemente distribuito | ||||||
Deformazione massima di una piastra circolare sottoposta ad un carico uniformemente distribuito
Consideriamo una piastra circolare con un raggio e lo spessore h. La piastra è fissata e sottoposto ad un carico uniformemente distribuito con il q intensità (vedi figura).
|
Il modello elementi finiti di una piastra circolare bloccato sotto un carico uniformemente distribuito (grande deviazione) |
Usiamo i seguenti dati iniziali: il raggio della piastra a 0,25 m, lo spessore della piastra h è 0,005 m, l'intensità q carico è 1E + 05 Pa.
Le proprietà del materiale sono E = 2.1E + 011 e n = 0,28.
Usiamo la seguente formula approssimata per calcolare gli spostamenti del centro piatto:
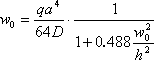 ,
,
dove
![]()
è la rigidezza flessionale della piastra.
Risolvendo questa equazione per w0, si ottiene il valore di deformazione massima, che è previsto al centro della piastra: w0 = 2.3258E-003 m.
Dopo aver effettuato i calcoli (tenendo conto della non linearità) dalla AutoFEM Analysis i seguenti risultati sono stati ottenuti (numero di step di carico è di 6):
Tabella 1.Parametri della mesh ad elementi finiti
Tipo di elementi finiti |
Numero di nodi |
Numero di Elementi Finiti |
Triangolo lineare |
921 |
1712 |
Triangolo quadratico |
3553 |
1712 |
Tabella 2. Risultato “Spostamento”
Spostamento (soluzione numerica) w0*, mm |
Spostamento (soluzione analitica) w0, mm |
Errore δ =100%*|w0*- w0|/| w0 | |
2.3286 |
2.3258 |
0.12 |
2.3042 |
2.3258 |
0.92 |
|
Conclusioni:
L'errore relativo della soluzione numerica rispetto alla soluzione analitica è pari al 0,92% per elementi finiti quadratici.
*I risultati dei test numerici dipendono dagli elementi finiti della maglia e possono differire leggermente da quelli indicati nella tabella.
Approfondire riguardo ad AutoFEM Static Analysis