Campo di temperatura non in regime di stato stazionario in una sfera isotropica

Consideriamo problema di determianzione di un campo di temperatura all'interno di una sfera isotropica nel volume da noi prescritto ad una temperatura iniziale Tstart=293.15 oK, e il quale è scaldato lungo la superficie esterna dove noi prescriviamo la temperatura costante a Tborder=373.15 oK (ad esempio, la sfera a temperatura ambiente è stata posta a temperatura inferiore al punto di ebollizione dell'acqua). Si determini la temperatura ad ogni punto della sfera (localizzata alla distanza r dal centro della sfera) al trascorrere del tempo secondo questi incrementi Δt1,2,3 = 10, 20, 30 secondi.

La sfera ha i seguenti parametri: raggio a =100 mm, densità del materiale 7800 kg / m3, calore specifico c = 440 J / (kg •oK), conduttività termica K=50 W / (m • oK).

Un gran numero di leghe metalliche hanno queste caratteristiche.

Per modelli numerici data la simmetria noi consideriamo 1/8 parte della sfera. Lo spicchio della sfera preso in considerazione ha il centro della sfera corrispondente ad  un vertice e su tutte le superfici di tale porzione vi è un flusso di calore pari a zero.

(si veda figura)

Consideriamo v essere la soluzione desiderata (campo di temperatura). Allora, dalla presa in considerazione che la soluzione non dipende dagli angoli di rotazione del vettore emanante dal centro della sfera (simmetry condition), noi possiamo performare il cambio di variabili nella forma v=r•u, dove r è la distanza dal centro della sfera, e u è qualche funzione. Dopo questo cambio di variabili, noi otteniamo l'equazione per u:

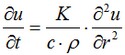
dove t è il tempo di raffredamento/riscaldamento del corpo solido. Le condizioni limite per u sono:

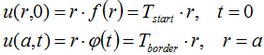
Dalla soluzione di questo problema dal metodo di separazione delle variabili, noi otteniamo l'espressione per v:

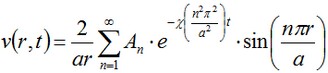
dove χ=K/(c•ρ) è il coefficiente di conduttività termica. I pesi An nell'espansione sono determinate dalla formula:

Confrontiamo la soluzione numerica con quella semi-analitica nel punto con raggio R1=0.5 m.

Nel dato punto noi compareremo la soluzione numerica ottenuta usando l'Analisi AutoFEM con la soluzione semi-analitica uno.

 

Poichè la soluzione alternativa è stata ottenuta dall'approccio semi-analitico (dall'estrazione di parziali somme della serie), è richiesto determinare il numero di cifre significanti quali possono essere usate per il confronto con la soluzione analitica. La tabella, data a seguire, mostra con quale accuratezza i calcoli sono stati computati per per ottenere soluzioni dall'espansione in serie e per costruzione della soluzione nel grafico.Conclusione sul numero di cifre signicative nella soluzione analitica possono essere fattedall'indicatore del cambiamento relativo nella soluzione e il fatto che la nostra serie sempre converge.

Dai calcoli effetttuati sono stati ottenuti questi risultati:

 

Tabella 1. Parametri degli elementi finiti della maglia

 

Tabella 2. Parametri del tempo di dscretizzazione

Tabella 3. Parametri del calcolo della soluzione semi-analitica ottenuta dall'espansione in serie

 

Per calcoli numerici noi prendiamo i risultati con N=7000. Per la costruzione di grafici noi usiamo i risultati con N=500.

Table 4. Risultati "Temperature"

 

Conclusioni:

Noi abbiamo ottenuto la figura realistica del campo di temperatura. Il relativo errore della soluzione numerica comparata alla soluzione analitica non supera lo 0.07% con elementi lineari a t=30 s. L'errore di calcolo è stabile nel tempo e non cresce significativamente quando il tempo computazionale è aumentato. Il grafico della temperatura in funzione del tempo mostra che la soluzione analitica e numerica coincidono.

L'errore di calcolo con elementi quadratici è più piccolo che non elementi lineari in un piccolo intervallo di tempo.

 

 

* I risultati dei test numerici dipendono dalla maglia ad elementi finiti e possono differire leggermente da quelli indicati nella tabella.

** Sui bordi dove le condizioni al contorno non sono specificate, la condizione di flusso di calore zero è soddisfatta automaticamente.

Approfondire riguardo ad AutoFEM Analisi Termica

 

 

Torna ai contenuti

autofem.com