Sfera cava radiante all'esterno

Consideriamo un problema di dterminazione dello stato stazionario del campo di temperatura di una sfera cava, sulla superficie interna della quale noi manteniamo una temperatura costante T1 =600 oK, e la superficie esterna raggia calore all'ambiente esterna. L'ambiente circostante ha la temperatura Tamb=290 oK. Per questa temperatura l'effetto della radiazione cambia significativamente la temperatura all'interno del volume del corpo. Noi possiamo determinare il campo di temperatura nei punti di controllo con raggi R123.

Caratteristiche della sfera: raggio esterno R=100 мм; raggio interno R/2=50 mm; la conduttività termica K=50 W/(m • oK); emissività della superficie sferica è uguale a α=1.

consideriamo uno spicchio pari ad 1/8 della sfera cava per ragioni di simmetria. Sulle superficie laterali dela sfera noi definiamo la superficie di flusso zero.

(si veda figura)

Poichè il materiale è isotropico, la soluzione al problema dipenderà solo dal raggio. Se l'origine del sistema di coordinate sferiche è posto al centro della sfera, noi otterremo l'equazione con condizioni limite:

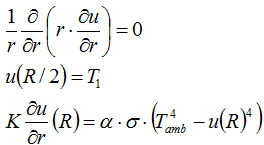
La soluzione dell'equazione ha la forma:

dove le costanti C1 e C2 sono determinate dalle condizioni limite nella via seguente:

La prima equazione (per i dati parametri) ha due radici reali. Per le radici: C1 = -4483.400605 e C2 = -12831.06789 la soluzione sul bordo ha la temperatura negativa sul bordo. Per la scala di Kelvin è impossibile ottenere temperature negative. Perciò solo le radici C1 = -13.02949201 e C2 = 560.9671302 soddisfano l'equazione.

Compariamo la soluzione numerica con quella analitica ai punti con raggio  R123=0.0707106; 0.0848528; 0.0989949 m (le coordinate dei sensori in questi punti X123=50; 60; 70 mm and Y123=50; 60; 70 mm).

Nei dati punti compareremo la soluzione ottenuta usando l'Analisi AutoFEM con la soluzione analitica.

I calcoli effettuati ci hanno permesso di ottenere i seguenti risultati:

Tabella 1. Parametri degli elementi finiti della maglia

Tabella 2. Risultati "Temperature"

 

Conclusioni:

L'errore relativo degli approcci di calcolo è 1.62%. Notiamo che quando la maglia è rifinita, la soluzione numerica approccia alla soluzione analitica lentamente a causa della non linearità del problema stesso.

Come noi vediamo, quando computando la radiazione, l'errore relativo è praticamente lo stesso per elementi lineari che quadratici. Questo può essere spiegato da l'errore nella soluzione di equazioni non lineari. Perciò, quando computando la radiazione, esso è sensato usare solo elementi lineari perchè è più piccolo il costo computazionale.

 

 

* I risultati dei test numerici dipendono dalla maglia ad elementi finiti e possono differire leggermente da quelli indicati nella tabella.

** Le radici sono state trovate con l'aiuto di Maple 9.5

 

Approfondire riguardo ad AutoFEM Analisi Termica

 

 

Torna ai contenuti

autofem.com