Piastra ortotropica di grafite in temperatura a regime di stato stazionario

Consideriamo adesso il problema di stato stazionario di conduttività termica per il calcolo del gradiente di temperatura (flusso di calore) attraverso una piastra ortotropica in materiale cristallino. Come esempio, si consideri una piastra rettangolare di grafite con conduttività termica di K1=278 W/(m•oK) lungo l'asse principale e K2 = 139 W/(m•oK) nella direzione perpendicolare all'asse principale. Le dimensioni sono a x b, con a=200 mm, b=100 mm, ed uno spessore di D = 2 mm. Uno dei bordi più corti della piastra è mantenuto a temperatura costante T1 = 353.15 oK , mentre i rimanenti bordi sono mantenuti a T2 = 273.15 oK. In regime di stato stazionario le temperature applicate non  subiscono variazioni nel tempo. La piastra scambia calore con l'ambiente circostante e quest'ultimo si trova a temperatura di 273.15 oK, il coefficiente di trasferimento di calore è H=400 W/(m2 • oK).

(si veda figura)

Per il dato problema l'equazione differenziale ha forma:

Questo problema può essere risolto nel piano di coordinate OXY su un dominio rettangolare [0,a]х[0,b], associato al piatto di grafite. La soluzione Analitica del problema è espressa in termini della serie di Fourier e ha la forma:

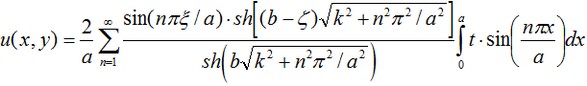
Le linee isotermiche delle soluzioni ottenute hanno la forma mostrata in Figura ottenute con Maple 9.5:

Consideriamo di localizzare dei sensore di temperatura come mostrato in Figura. Le temperature campionate verranno comparate con la soluzione numerica ottenuta usando l'Analisi AutoFEM con la soluzione analitica.

Si noti che i punti vicini al bordo non devono essere selezionati come termini della serie di Fourier ( 200 termini in una somma è accettabile per 8 10 nm). La serie di Fourier valutata  nei punti al contorno va a convergenza con grandi oscillazioni. Il linea generale in una serie di Fourier per ottenere la migliore accuratezza, è necessario aumentare il numero di termini della serie inserendo come termini delle somme parziali di serie.

Dai calcoli sono stati ottenuti questi risultati:

Tabella 1. Parametri della maglia finita

Tabella 2. Resultati "Temperature"

 

Conclusioni:

Il relativo errore della soluzione numerica comparata con la soluzione analitica non eccede lo 0.02% per i punti in sequenza lineare. Il presente metodo è stato provato essere efficace quando risolvendo i problemi con anisotropa distribuzione di temperatura. L'esistenza di proprietà ortotropiche non non ha influito sull'efficienza computazionale efficienza del metodo. Il grafico della dipendenza della temperatura sulla distanza mostra che la soluzione analitica e numerica coincidono da un punto di vista pratico. Questo implica che le distribuzioni dei massimi e minimi della temperatura sono identiche, e perciò, il calcolo del flusso di calore e la potenza avranno lo stesso grado di accuratezza.

 

* I risultati dei test numerici dipendono dalla maglia ad elementi finiti e possono differire leggermente da quelli indicati nella tabella.

 

Approfondire riguardo ad AutoFEM Analisi Termica

 

 

Torna ai contenuti

autofem.com