 |
AutoFEM Analysis Análisis estático | ||||||
Análisis estático
El objetivo principal del análisis resistencia estática de las estructuras es la evaluación de un estado de estrés de una estructura sometida a fuerzas constante en el tiempo (estáticos). Esta evaluación del estado de estrés se realiza generalmente con el fin de sondear las características de diseño adoptadas contra el criterio de resistencia. El criterio de resistencia se formula generalmente como sigue:
Desarrollo del estrés σ en una estructura bajo fuerzas externas aplicadas debe ser inferior a la tensión de seguridad [σ ] para el material estructural dada después de aplicar el margen de tensión de factor de seguridad ksafe.
![]()
El módulo de análisis estático del sistema de modelado de elementos finitos AutoFEM sirve para calcular un estado de tensión estática de las estructuras tridimensionales en el entorno AutoCAD. El módulo de análisis estático trabaja directamente con modelos de AutoCAD en tres dimensiones y no requiere construcciones adicionales para la resolución de un modelo tridimensional en particular.
Los principales resultados de una solución estática son:
| • | Campo de desplazamientos de la estructura en los puntos de cálculo de la malla de elementos finitos; |
| • | Campo de deformación relativa; |
| • | Componentes de la tensión sobre el terreno; |
| • | Energía de deformación; |
| • | Respuesta del nodo (fuerzas de reacción); |
| • | El campo de la distribución factor de seguridad cepa sobre el volumen de la estructura; |
| • | Estimación del error de estrés; |
Estos datos es normalmente suficiente para predecir el comportamiento de la estructura y la toma de decisiones para optimizar la forma geométrica de una parte con el objetivo de asegurar los principales criterios de resistencia de las piezas.
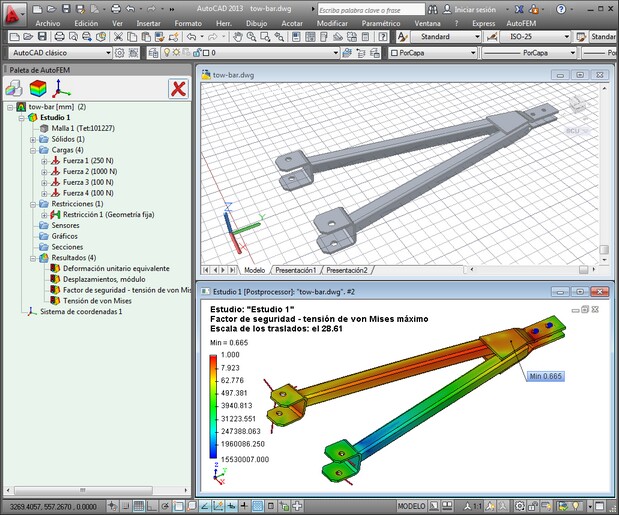
Los detalles de los pasos de análisis estático
Análisis estático de un modelo se lleva a cabo en varias etapas. Se enumeran los elementos necesarios para realizar un análisis.
Para ejecutar un análisis estático, siga los siguientes pasos:
Paso 1. Creación de modelo sólido tridimensional de una parte.
Antes de empezar a trabajar en el sistema de AutoFEM, usted debe preparar un modelo sólido tridimensional para ser evaluado. Un modelo sólido se puede construir en el entorno de AutoCAD o importados de otros sistemas. El análisis estático puede realizarse sobre una o varias operaciones de los cuerpos.
Paso 2. La creación de "Estudio".
Puede utilizar una de las siguientes formas de crear estudio:
Linea de comando: |
_FEMASTUDY |
Menú principal: |
AutoFEM | Crear un estudio... |
Icono: |
|
También es necesario especificar el tipo ( " Análisis estático ") del estudio en la ventana de propiedades del sistema.
Si hay varios cuerpos en la escena, entonces usted necesita para seleccionar uno o varios cuerpos en contacto, por el que se creará un nuevo estudio.
Paso 3 . Material que define.
Uno de los elementos necesarios de cualquier solución es materia de estudio. Descripción detallada de los métodos de material que define para los cálculos se proporciona en la sección respectiva de la descripción preprocesador.
Paso 4 . Creación de malla.
Para llevar a cabo la modelización de elementos finitos, es necesario construir una malla de elementos finitos. Por defecto, el comando de construcción de malla inicia automáticamente cuando se crea un estudio. El usuario también puede crear una malla con el comando AutoFEM " AutoFEM | Crear malla... ". Al crear una malla, el usuario define diversos parámetros de discretización de un modelo de estado sólido. La malla de elementos finitos puede influir significativamente en la calidad de la solución obtenida en los casos de complejo configuración espacial de las piezas. Los parámetros finitos generación de malla de elementos se analizan en detalle en la sección respectiva de AutoFEM preprocesador descripción.
Paso 5 . La aplicación de las condiciones de contorno.
En el análisis estático, condiciones de contorno están representados por métodos de sujeción y las cargas externas aplicadas al sistema. Las condiciones de frontera que crean el escenario es muy importante y requiere una buena comprensión por parte del ingeniero de la esencia del estudio está resuelto. Por lo tanto, pensar en los aspectos físicos del estudio a fondo antes de la aplicación de las condiciones de contorno.
Definición de las restricciones es una condición necesaria para la ejecución de un análisis estático correcto. La limitación en el movimiento combinado de los cuerpos deberán cumplir las siguientes condiciones:
Para tener una carcasa para un análisis estático, un modelo debe tener restricciones que impiden la libre circulación en el espacio como un cuerpo sólido. El no cumplir con esta condición provocará resultados incorrectos de análisis de elementos finitos o el aborto de los cálculos.
Un comando se proporciona en AutoFEM para definir restricciones: "Fixture ". El tipo " fijo" de los sistemas de retención define un estado (inmueble ) totalmente fijo para el elemento del modelo seleccionado. El tipo "General" de las restricciones permite limitar modelo de elementos de movimiento a lo largo de los ejes del sistema de coordenadas elegido.
El comando "Fixture " también proporciona otra funcionalidad útil. No es un recurso para especificar desplazamientos conocidos para la estructura en ella. Para ello, especifique el valor de caudal fijo de un elemento del modelo a lo largo de algunos de los ejes de coordenadas en el "Fixture " ventana de propiedades del sistema. Análisis estático se realizará con esta enfermedad representó. Tenga en cuenta que una solución estática es posible en este caso sin la aplicación adicional ( fuerza) de las cargas. De esta manera, se puede evaluar el estrés en desarrollo en una estructura tensa cuando se conocen los valores cuantitativos de la cepa ( desplazamientos ).
|
|
Ejemplo de utilización de desplazamientos conocidos |
|
Una serie de comandos especializados se proporciona en AutoFEM definir cargas; quienes permiten definir los principales tipos de cargas ("fuerza", "Presión", "fuerza centrífuga", "Aceleración", "La Carga", "Torque"). Descripción detallada de todos los tipos de cargas se proporciona en la descripción preprocesador.
Nota uno más capacidad funcional de una solución estática en AutoFEM. El usuario puede definir el análisis de estado de estrés de una estructura no sólo en virtud de diversas fuerzas, sino también bajo cargas térmicas - el Estudio "termoelasticidad". Como es sabido, los materiales estructurales desarrollan tensión lineal bajo el impacto térmico - ampliar radiante y reducir enfriando. Los cambios en las dimensiones de un cuerpo causan tensión y un estado de estrés. AutoFEM representa los cambios de temperatura. Para definir las temperaturas en la contabilización de los campos de temperatura transitoria, utilice el comando:
Linea de comando: |
_FEMATEMP |
Menú principal: |
AutoFEM | Cargas/Restricciones | Temperatura... |
Icono: |
|
Al mismo tiempo, es necesario habilitar la opción "Considerar los efectos térmicos" en la ficha [termoelasticidad] del cuadro de diálogo parámetros de estudio estática con el fin de dar cuenta de las cargas térmicas en la solución estática. Usted también tendrá que definir la temperatura de la tensión "cero", que corresponde al estado de no-estrés de la modelo, y para definir el campo de temperatura de trabajo (detalles en la sección "Configuración de lineales Estática procesador").
Paso 6. Ejecución de cálculos.
Una vez que una malla de elementos finitos se construye para el modelo y las condiciones de contorno son aplicadas (restricciones y cargas), puede iniciar el proceso o la creación y la resolución de ecuaciones algebraicas lineales del análisis estático. Utilice el comando siguiente para iniciar la solución del estudio activo:
Linea de comando: |
_FEMASOLVE |
Menú principal: |
AutoFEM | Resolver... |
Icono: |
|
El cálculo estudios seleccionados se puede iniciar desde el menú contextual al hacer clic ![]() en el nombre del estudio seleccionado en el árbol de estudios.
en el nombre del estudio seleccionado en el árbol de estudios.
Por defecto, el " Estudio de los parámetros " de diálogo del análisis estático se abre automáticamente antes de los cálculos. En este cuadro de diálogo, el usuario puede definir las opciones y configuraciones de la solución deseada, así como especificar los tipos de datos en el boton solución en el árbol de estudios. Descripción detallada de la finalidad del estudio es aún más ajustes disponibles en la sección " Configuración de lineales Estática procesador". La mayoría de los ajustes se seleccionan por el procesador de forma automática en función del número de dimensiones en el estudio que se está resuelto e impusieron condiciones de contorno.
Al hacer clic en el botón [ Aceptar] en el cuadro de diálogo parámetros de estudio se inicia el proceso de construcción y los sistemas de resolución de ecuaciones algebraicas lineales. Las etapas de la solución de ecuaciones e información adicional de referencia se muestran en un panel de información especial. Al hacer clic en el botón [ Cerrar] en el panel de información termina cálculos. La bandera " Cerrar el diálogo en la resolución de complexión " forzará el cierre automático de la solución de los pasos ventana de monitoreo después de terminar la resolución de ecuaciones.
La bandera « Guardar documento en la resolución de finalización » obligará a guardar automáticamente los resultados de los cálculos y todos los datos modificados en el documento activo.
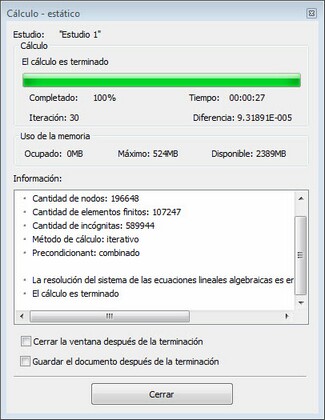
Los siguientes datos de referencia es de salida en la ventana de información:
Nodos - el número de nodos en la malla de elementos finitos computacional.
Elementos - el número de tetrahedrals en la malla de elementos finitos.
Argumentos - el número de ecuaciones de la estática lineales.
Tipo de cálculo - el algoritmo utilizado para resolver ecuaciones. Tipos de posibles algoritmos y su uso se describen en la sección " Configuración de lineales estática procesador".
Solución Total - dice que el sistema de ecuaciones se calculó con éxito. También existe información auxiliar en los soportes: inter - númericos de iteración ejecutada ( si se utilizó método iterativo ), tol - error de cálculo del resultado después de cálculo.
Para el solucionador de iteración, se presentan el número de la iteración actual y el error residual de la solución. Para el método directo, se muestra el porcentaje del número total de las ecuaciones resueltas. El usuario puede ver en el modo en tiempo real, lo que es la tasa de resolución de ecuaciones, y gestionar este proceso. Además, para ambos métodos de resolución, tres parámetros se muestran, que caracterizan a la necesidad de la memoria operativa: ¿qué cantidad de memoria está ocupada por el solver en la actualidad, el uso máximo, y la cantidad de memoria operativa gratuita está disponible en el sistema en este momento. Estos parámetros permiten que cada usuario pueda evaluar si su su sistema / equipo se ajusta a la solución de un problema particular.
Los pasos de cálculo también se muestran visualmente como una escala de actualización dinámica. Además, se muestra el tiempo transcurrido desde el inicio de los cálculos. Tras finalizar los cálculos, el usuario debe cerrar la ventana auxiliar ( a menos que la opción de cierre automático está activado ).
Paso 7. Análisis de los resultados solución estática.
Después de completar los cálculos, una nueva carpeta de "Resultados" aparece en el árbol de estudios. Por defecto, éste muestra los resultados definidos en la pestaña " Resultados " del cuadro de diálogo "Parámetros de estudio ". En general, el usuario puede acceder a 38 soluciones en el resultado del análisis estático, resuelto en 6 grupos.
Grupo "Desplazamientos" incluye los siguientes resultados.
![]() - De componentes de vector de desplazamiento para un nodo de la malla de elementos finitos lo largo del eje OX del sistema de coordenadas mundial;
- De componentes de vector de desplazamiento para un nodo de la malla de elementos finitos lo largo del eje OX del sistema de coordenadas mundial;
![]() - De componentes de vector de desplazamiento para un nodo de la malla de elementos finitos lo largo del eje OY del sistema de coordenadas mundial;
- De componentes de vector de desplazamiento para un nodo de la malla de elementos finitos lo largo del eje OY del sistema de coordenadas mundial;
![]() - e componentes de vector de desplazamiento para un nodo de la malla de elementos finitos lo largo del eje OY del sistema de coordenadas mundial.
- e componentes de vector de desplazamiento para un nodo de la malla de elementos finitos lo largo del eje OY del sistema de coordenadas mundial.
Desplazamientos valor absoluto, - el valor absoluto de los desplazamientos nodales del modelo, definido para cada nodo de acuerdo con la fórmula:![]() ,donde x, y, z - componentes del vector de desplazamiento para el nodo i-ésimo de la malla de elementos finitos.
,donde x, y, z - componentes del vector de desplazamiento para el nodo i-ésimo de la malla de elementos finitos.
Grupo «Destaca» incluye los siguientes resultados:
![]() -tensiones equivalentes relativos evaluados a partir de componentes del tensor de tensiones de acuerdo con la fórmula:
-tensiones equivalentes relativos evaluados a partir de componentes del tensor de tensiones de acuerdo con la fórmula:![]() ;
;
![]() -Tensión normal en la dirección del eje OX del sistema de coordenadas mundial;
-Tensión normal en la dirección del eje OX del sistema de coordenadas mundial;
![]() - Tensión normal en la dirección del eje OY del sistema de coordenadas mundial;
- Tensión normal en la dirección del eje OY del sistema de coordenadas mundial;
![]() - Estrés normal en la dirección del eje OZ del sistema de coordenadas mundial;
- Estrés normal en la dirección del eje OZ del sistema de coordenadas mundial;
![]() - Tensión de cizallamiento que actúa en la dirección del eje OY del sistema global de coordenadas en un plano con el vector normal paralela al eje OX;
- Tensión de cizallamiento que actúa en la dirección del eje OY del sistema global de coordenadas en un plano con el vector normal paralela al eje OX;
![]() - Tensión de cizallamiento que actúa en la dirección del eje OZ del sistema de coordenadas global en un plano con el vector normal paralela al eje OX;
- Tensión de cizallamiento que actúa en la dirección del eje OZ del sistema de coordenadas global en un plano con el vector normal paralela al eje OX;
![]() - Tensión de cizallamiento que actúa en la dirección del eje OZ del sistema de coordenadas global en un plano con el vector normal paralela al eje OY;
- Tensión de cizallamiento que actúa en la dirección del eje OZ del sistema de coordenadas global en un plano con el vector normal paralela al eje OY;
![]() -tensiones principales
-tensiones principales ![]() .
.
Intensidad de estrés: Se define de la siguiente manera: ![]()
Estimación del error estrés. Este resultado muestra la estimación del error de cálculo de las tensiones en los porcentajes. La estimación se representa como valor del elemento (constante dentro de un solo tetraedro). Valor de error grande del elemento significa que no es la gran diferencia en el cálculo de las tensiones con sus elementos vecinos. El resultado más fiable de cálculo de la tensión se logra cuando la estimación de error de la tensión tiende a una distribución uniforme. Para obtener más información acerca de la estimación de error, consulte la Revista Internacional de Métodos Numéricos en Ingeniería, vol. 24, 337-357 (1987) "Un error Estimador Simple y Procedimiento de adaptación para el Análisis de Ingeniería Práctica" por el OC Zienkiewicz y J. Z. Zhu)..
«Factor de seguridad por las tensiones» Grupo incluye los siguientes resultados:
Factor de seguridad por tensiones equivalentes representa la relación entre admisible para un determinado tensiones del material estructural [σ ] a las tensiones equivalentes:
![]()
Factor de seguridad por esfuerzos de corte se evalúa como:
![]()
Factor de seguridad por tensiones normales se evalúa como:
![]()
Estrés segura de un material se define en las propiedades de los materiales en la biblioteca estándar de AutoCAD o en el campo adecuado de los materiales de la biblioteca del estudio. El límite elástico es aceptado como el estrés seguro para materiales plásticos.
Grupo « deformación » incluye los siguientes resultados:
![]() - cepas equivalentes relativos expresados en términos de componentes del tensor de deformaciones por la fórmula:
- cepas equivalentes relativos expresados en términos de componentes del tensor de deformaciones por la fórmula:
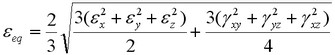 ;
;
![]() - relativa cepa normal en la dirección del eje OX del sistema de coordenadas mundial;
- relativa cepa normal en la dirección del eje OX del sistema de coordenadas mundial;
![]() -relativa cepa normal en la dirección del eje OY del sistema de coordenadas mundial;
-relativa cepa normal en la dirección del eje OY del sistema de coordenadas mundial;
![]() -relativa cepa normal en la dirección del eje OZ del sistema de coordenadas mundial;
-relativa cepa normal en la dirección del eje OZ del sistema de coordenadas mundial;
![]() - deformación de corte en el plano OXY;
- deformación de corte en el plano OXY;
![]() - deformación de corte en el plano OXZ;
- deformación de corte en el plano OXZ;
![]() -deformación de corte en el plano OYZ.
-deformación de corte en el plano OYZ.
![]() - deformaciones principales
- deformaciones principales ![]() .
.
Densidad de Energía de Deformación. El resultado refleja la distribución de volumen de energía de deformación sobre el modelo.
Grupo «reacciones». El resultado refleja las fuerzas se acumulan en los nodos de apoyo (fijo) del modelo de elementos finitos.
![]() -reacción de la fuerza en la dirección del eje OX del sistema de coordenadas mundial;
-reacción de la fuerza en la dirección del eje OX del sistema de coordenadas mundial;
![]() - Fuerza de reacción en la dirección del eje OY del sistema de coordenadas mundial;
- Fuerza de reacción en la dirección del eje OY del sistema de coordenadas mundial;
![]() - fuerza de reacción en la dirección del eje OZ del sistema de coordenadas mundial;
- fuerza de reacción en la dirección del eje OZ del sistema de coordenadas mundial;
La fuerza de reacción (valor absoluto) - la magnitud del valor absoluto de las fuerzas de reacción nodales del modelo definido para un nodo como ![]() , donde
, donde ![]() - x
- x
-componente, ![]() - y-componente,
- y-componente, ![]() – z-componente de la fuerza de reacción para el nodo i-ésimo de la malla de elementos finitos.
– z-componente de la fuerza de reacción para el nodo i-ésimo de la malla de elementos finitos.
Grupo "carga total" muestra las cargas aplicadas a un modelo de elementos finitos como las respuestas de nodo eficaces. Este tipo de datos representa la información de referencia.
Temperatura. Este resultado muestra la distribución de campo de la temperatura sobre el volumen del modelo.
Algoritmo de análisis estático
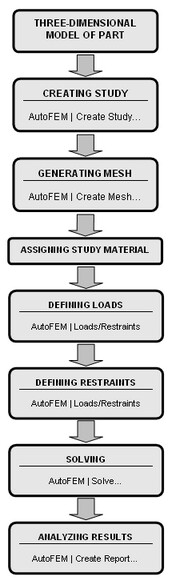
Algoritmo para la evaluación de la resistencia estática basada en Modelado
Una vez que el cálculo de estudio se completa con éxito, usted debe analizar los resultados obtenidos con el fin de llegar a conclusiones sobre la fuerza estática probabilística de la estructura. En la mayoría de los casos, tres tipos de solución son suficientes - desplazamientos, tensiones y el factor de seguridad de deformación. Una secuencia típica de los pasos para la validación de los resultados de la modelización de elementos finitos es la siguiente:
| 1. | Análisis Desplazamiento. En el árbol de los estudios, use la opción del menú contextual "Abrir" o "Abrir en ventana nueva " para abrir el " Desplazamiento magnitud " solución. Podemos estimar visualmente el patrón y los rangos del estado de tensión-deformación de una estructura. Es necesario analizar los desplazamientos con el fin de verificar correctnes de cargas aplicadas y afirmar la corrección de la solución encontrada como resultado de resolver sistemas de ecuaciones. Si los resultados del análisis de los desplazamientos indican que una solución para el estudio se encuentra y el modelo de estado de deformación de la estructura que coincide con el esperado, entonces usted puede proceder con el siguiente paso.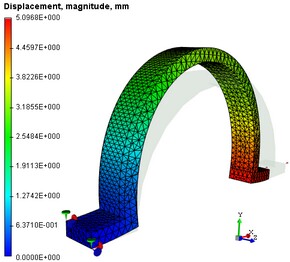 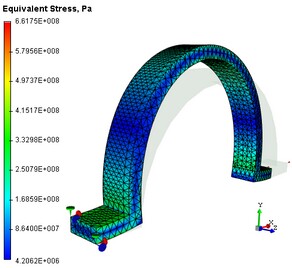 |
El diagrama de desplazamientos absolutos y tensiones equivalentes
| 2. | Análisis de tensión. Abra el " esfuerzo equivalente " número. Se puede evaluar visualmente el patrón de la tensión equivalente calculado. Los gradientes de estrés se ilustran mediante transiciones de color. La escala de código de color que se muestra en la ventana de resultados de cálculo vista ayuda a leer el valor aproximado del resultado mostrado. Si apunta el ratón a la zona de interés en el modelo, y luego una pista aparezca, mostrando el valor de la medida evaluada, interpolado por los nodos más cercanos alrededor de la posición del puntero. El " estrés Equivalente " número permite al usuario realizar las siguientes conclusiones: |
a) Determinar, en qué lugares y en qué elementos de la estructura de la mayor tensión se desarrolla ;
b ) Mediante la comparación de los máximos de las tensiones calculadas con el esfuerzo admisible para el material del modelo, se puede evaluar el grado de la resistencia estructural.
| 3. | Estimación del factor de seguridad. Abra el " Factor de seguridad equivalente por el estrés " número. Este resultado permite la estimación de la relación cuantitativa de la tensión segura a las tensiones equivalentes calculados especificados en las propiedades del material. Por defecto, el resultado se muestra en la escala logarítmica con el fin de reducir el rango de gradientes de color. Si la relación de las tensiones seguras y calculados se acerca a uno o llega a ser menos que eso, entonces el criterio de resistencia ya no se sostiene y, por lo tanto, el diseño debe ser alterado. |
Configuración del procesador lineal y no lineal estática
Las propiedades de estudio definidos por el usuario se guardan junto con el documento y se heredan en la copia de un estudio. El objetivo principal de las propiedades del estudio es definir las opciones necesarias para el procesador, los listados de resultados que se mostrarán después de completar los cálculos en el árbol de los estudios, así como mantener los atributos descriptivos del estudio, como su nombre o un comentario. El diálogo de parámetros de la solución de análisis estático tiene cinco fichas.
La ficha [General] sirve para la definición de propiedades descriptivas del estudio actual.
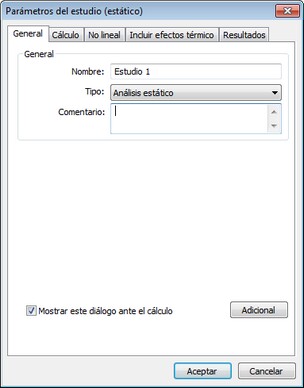
En el campo "Nombre", el usuario puede editar el nombre de estudio asignado el sistema por defecto en la creación. Este nombre será aún más en el que se muestra en el árbol de los estudios, en la ventana de resultados y en el informe. El control "Tipo" sirve para definir el tipo de estudio. Tenga en cuenta que AutoFEM permite cambiar un tipo de estudio existente a otro uno de la lista de tipos de estudio disponibles para el usuario. Por ejemplo, el usuario puede crear un estudio de tipo "Análisis estático", y luego cambiar el tipo, por ejemplo, a "la estabilidad" o "análisis de frecuencia".
El cuadro de edición "Comentario" permite al usuario introducir información de texto arbitrario perteneciente al estudio actual. Esta información será utilizada en el futuro para la generación de un informe basado en los resultados de la solución de estudio.
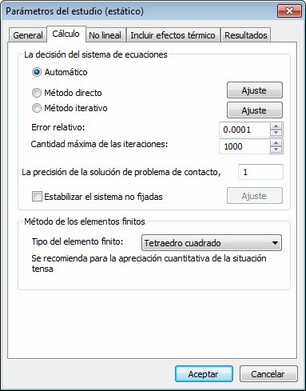
La ficha [ Resolver ] sirve para definir las propiedades del procesador para la solución de ecuaciones lineales estáticas. Los elementos de control en el grupo de " método de cálculo" permite al usuario definir los métodos de sistemas de ecuaciones algebraicas lineales de la estática resolver.
Automático. El solucionador elige el método de resolución de ecuaciones basados en el número de ecuaciones. Si el número de ecuaciones supera el umbral establecido en la Configuración de la cuenta AutoFEM (el valor predeterminado se establece en 100.000 ), el sistema de ecuaciones se resuelve mediante un método iterativo, si el número de ecuaciones es menor que el límite especificado, el método directo de se elige solución.
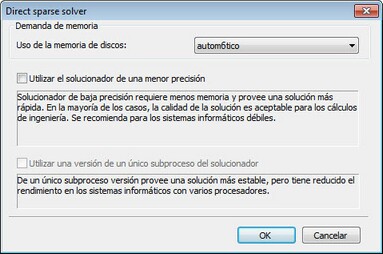
Método directo. El sistema de ecuaciones se resuelve por el método de Gauss a través de la descomposición LU de la matriz de rigidez. Este método es eficaz para resolver el sistema de ecuaciones construidas sobre la base de los elementos finitos lineales. En ciertos casos, el uso del método directo puede ser también justificado para el análisis del sistema con la ayuda de elementos finitos cuadráticas. Se puede utilizar en lugar de método iterativo, si el algoritmo iterativo no converge a la solución estable, o si la velocidad de convergencia es muy pequeño ( el número de iteraciones es varios miles ). Esta situación se puede observar para los problemas de « finas » ( el modelo es plana o estirado ), y también, para un gran número de elementos finitos, que son considerablemente diferentes de elementos equiláteros ( cuando la relación de las longitudes de los bordes de elementos finitos son en del orden de cientos o miles ). Ajustes adicionales del método directo son disponibles ("Opciones " botón )
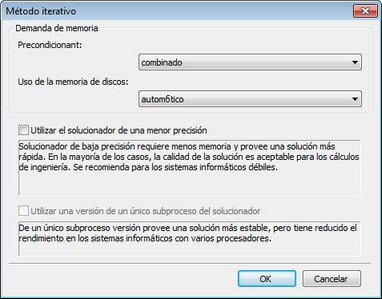
Iterativo. Los sistemas de ecuaciones se resuelven por métodos iterativos. Este método se utiliza por defecto para los sistemas de ecuaciones, construidas sobre la base de un elemento finito cuadrática para resolver. Las dos opciones siguientes se pueden establecer para el método iterativo: la tolerancia relativa y el número máximo de iteraciones. Ajustes adicionales del método iterativo están disponibles ("Opciones")
El uso adicional de memoria de disco. El usuario también puede gestionar la interacción con (disco) externo de memoria del sistema informático en la resolución de ecuaciones mediante un método directo o iterativo ( [Opciones] ). Hay tres opciones para el uso de memoria de disco adicional: automático, no disponible, obligatorio. El uso de la memoria de disco adicional le permite guardar la memoria de disco adicional matriz de rigidez decomposition.Using para resolver sistemas de ecuaciones es necesario sólo cuando la memoria necesaria para el mantenimiento de las matrices intermedias excede la memoria RAM del ordenador. Tenga en cuenta también que el tiempo de ejecución para los estudios con un gran número de dimensiones, utilizando almacenamiento externo podría ser significativa debido a un gran número de operaciones sobre los datos secuenciales de lectura-escritura.
Pueden ser necesarios grandes volúmenes de almacenamiento en disco para mantener matrices intermedias (hasta varios gigabytes ). Asegúrese de que hay suficiente espacio en disco antes de resolver los estudios de grandes dimensiones mediante almacenamiento externo.
Si el usuario deshabilita la posibilidad de utilizar el espacio en disco, mientras que la solución de un sistema de alta resolución de ecuaciones, una terminación anormal del proceso puede abortar cálculos en el caso de que el consumo de memoria para guardar la descomposición de la matriz se acerca 2 Gigabyte (para Windows de 32 bits ).
La opción de iniciar el solucionador de baja precisión. Este modo consume casi por tercera cantidad más baja de la memoria operativa y, además, los cálculos vaya más rápido. En la mayoría de los casos, se proporciona la precisión de la resolución de ecuaciones que es suficiente para los cálculos de ingeniería. Esta opción se puede aplicar si el usuario tiene una computadora lo suficientemente alimentado. Por defecto, se utiliza el solucionador de precisión normal. Además, es posible ejecutar el solucionador de baja precisión en un solo modo del procesador.
Tipo de preacondicionador (para el método iterativo). Cuatro tipos de preacondicionadores están disponibles. Preacondicionador combinado es el método más rápido y de forma predeterminada. Consume máxima cantidad de memoria. Descomposición Incompleta, se necesita una memoria adicional, que cantidad es igual la memoria ocupada por la matriz de rigidez. Diagonal e Identidad Preacondicionador, que prácticamente no utilizan memoria adicional, pero ofrecen una menor tasa de convergencia.
La precisión relativa - la exactitud de la solución iterativa logrado. Cuanto más pequeño es el error de cálculo de error especificado, se requerirá que el mayor número de pasos (iteraciones).
Número máximo de iteraciones - el número crítico de iteraciones, después de alcanzar el que la resolución iterativa del sistema de ecuaciones termina, incluso si no se logró la precisión solución requerida.
Precisión de la solución de restricciones de contacto. Este parámetro especifica el porcentaje relativo de los nodos Comunicación con que están excluidos en cada paso del proceso iterativo durante el cálculo de las condiciones de contorno de contacto. El valor mínimo es 1%, máximo 50%. Desde el punto de vista del usuario, un valor más pequeño retrasa la solución del problema de contacto, aunque la precisión de la solución se incrementa.
Estabilizar el modelo no fijado. Estabilizar el modelo no fijado. Por lo general, es imposible el cálculo de la resistencia estática de modelo no fijada, que se equilibra sólo por las fuerzas,. Debido a errores de redondeo el modelo se desplaza en el espacio o rota. Estos desplazamientos son significativamente mayores que las deformaciones que se producen en el modelo como resultado de la acción de las fuerzas estáticas y no nos permiten estimar el estado de tensión-deformación del sistema. Esta bandera activa la estabilización del modelo no fijado en el espacio. El principio de la estabilización es la siguiente. En todos los quilates del modelo se aplican muelles blandos imaginarios. Se supone que la rigidez de los muelles es insignificante en comparación con la rigidez del material a partir del cual se hizo el cuerpo. Por lo tanto, no afectan de manera significativa en el resultado del cálculo estático. Pero aquí surge no permiten el modelo se mueva sin control en el espacio. El usuario puede elegir un valor aceptable de la rigidez para estabilizar el sistema en cada caso práctico.
Methodos de Elementos Finitos . Por defecto, todos los cálculos se utilizan aproximación cuadrática para desplazamientos, sin tener en cuenta qué tipo de malla de elementos finitos se construyó para el modelo. Si el usuario sólo está interesado en los resultados cualitativos, es decir, él sólo está interesado en la distribución relativa de los campos de esfuerzos, utilizando una malla más fina, a continuación, se puede utilizar la solución de elementos lineales, que va mucho más rápido que la contraparte cuadrática. El elemento híbrido se utiliza para el análisis de la resistencia estática de los modelos que contienen ambos elementos en forma de placa y de volumen 3D lineales (los llamados modelos «híbrido»).
El análisis de elemento lineal tetraédrica proporciona una precisión insuficiente de los resultados cuantitativos. Desplazamiento y tensión máximos resultados son mucho más pequeñas a través del cálculo por elementos finitos tetraédricos lineales, más que los logrados por métodos más precisos. Se recomienda encarecidamente el uso de cálculos de elementos de segundo grado para la evaluación cuantitativa (el modo por defecto).
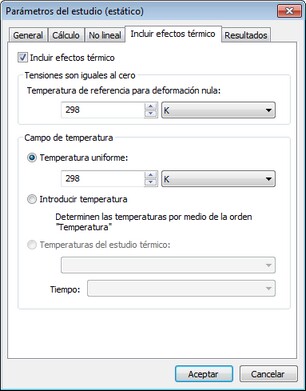
La ficha [ Incluir efectos térmicos ] permite definir los métodos de cálculo de cargas térmicas.
Incluir efectos térmicos. Incluye el modo de cálculo de las cargas en la construcción de una estructura debido a las fuerzas de expansión lineales bajo la condición de aplicación de calor en el cuerpo.
Temperatura de cero deformaciones: - la temperatura corporal inicial, en la cual no hay deformación térmica y no hay estrés causado por la diferencia de temperaturas. El usuario puede especificar los valores de temperatura en una de las escalas existentes: K - kelvin ; C - Celsius ; F- Farenheit. Definir el método de especificar las cargas térmicas en los "campos de temperatura " del grupo.
Uniforme de la temperatura - el valor de un campo uniforme de la temperatura se especifica en las unidades elegidas, lo que afecta a todos los órganos estudiados.
Utilice temperatura preestablecida - cargas térmicas se incluyen en el análisis estático, que se define mediante el comando " AutoFEM | Cargas / Restricciones | Temperatura ".
Utilice los resultados de calor en tareas - solución disponible del estudio de análisis térmico se utiliza para definir la carga térmica. En la lista desplegable, seleccione el nombre del estudio de análisis térmico resuelto y (si es necesario) en el instante en el tiempo, a la que pertenece la solución. Por favor, tenga en cuenta que ciertas condiciones deben cumplirse para el uso de los resultados de análisis térmico como las condiciones iniciales de temperatura:
| 1. | Condición de identidad de mallas de elementos finitos en análisis estáticos y térmicas. La forma más sencilla de conseguir dicha identidad es el uso de la opción "Copiar ", disponible en el menú contextual. La secuencia de pasos puede ser, por ejemplo, de la siguiente manera: |
a) Crear un estudio de tipo " Análisis Térmico ", generar una malla, definir las condiciones de frontera, y ejecutar ;
b) Crear una copia del estudio con el comando " Copiar" ;
c) En la pestaña "General" en el diálogo de propiedades del estudio, ha cambiado el tipo de estudio al " análisis estático ".
Como resultado, tenemos dos estudios de diferentes tipos, pero con idénticas mallas de elementos finitos.
| 2. | El " Cálculo utilizando lineal elemento " propiedad en la pestaña "Solve " del diálogo de parámetros de estudio debe utilizar la misma configuración en ambos estudios. Por ejemplo, si el análisis térmico se realiza por elementos lineales, entonces el análisis estático basado en resultados de análisis térmico puede también ser ejecutado solamente por elementos lineales. |
La ficha [Resultados ] permite definir los tipos de resultados que se pueden mostrar en el árbol de los estudios después de terminar los cálculos.
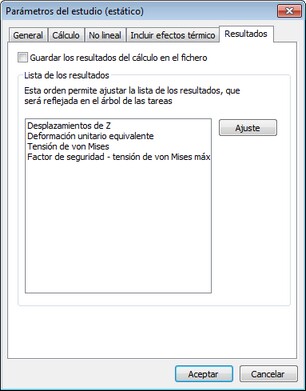
Guarde la solución de los resultados en el archivo - Activa el modo en el que todos los resultados del análisis se guardan en el archivo junto con el modelo. Esto permite analizar los resultados de un estudio anterior calculado y salvado sin la necesidad de un nuevo cálculo. Tenga en cuenta que el ahorro de los resultados de cálculo en un documento aumenta el tamaño del archivo de documento en aproximadamente 4,5 a 5 Mb por cien mil grados de libertad.
La ficha [No lineal] permite al usuario llevar a cabo el análisis estático de tomar en consideración los grandes desplazamientos.
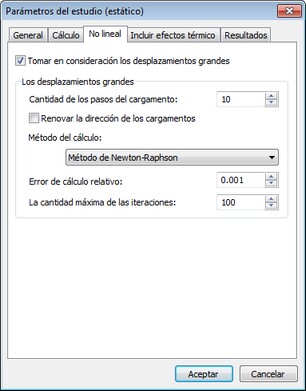
En la práctica, hay situaciones en las que los desplazamientos de determinados puntos de la estructura alcanzan valores significativos bajo la acción de cargas externas. Estos problemas son especialmente importantes en la industria aeronáutica y espacial, en el diseño de radiotelescopios, torres de refrigeración y otras estructuras de paredes delgadas. En estos casos, los efectos no lineales se deben tomar en consideración, ya que los supuestos en que se basa el análisis lineal no son válidas.
La opción " Usar formulación gran desplazamiento " se debe activar en los casos en que al menos uno de los siguientes supuestos del análisis lineal se viola:
1. Deformaciones resultantes son suficientemente pequeñas, por lo que los cambios de rigidez causados por la carga pueden ser ignorados ;
2. En el proceso de aplicación de la carga, condiciones de contorno no cambian la amplitud, la dirección y distribución.
Por ejemplo, el análisis lineal del tipo espiral parte sujeta a la carga aplicada en el borde extremo da un error de aproximadamente 30 % en comparación con el análisis no lineal. Esta diferencia en los resultados surge debido a la pequeña supuesto de desplazamiento adoptada en el análisis lineal.
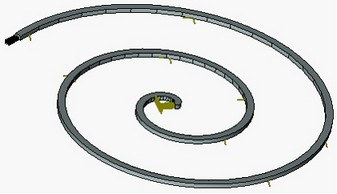
|
|
Análisis lineal |
El análisis no lineal |
Los controles en el grupo « no linealidad geométrica » permiten al usuario personalizar el proceso de solución de problemas geométricamente no lineal.
Para resolver tales problemas, un tiempo de paso a paso solucionador no lineal organiza el proceso de carga incremental de la estructura y da la solución del sistema de ecuaciones linealizado de en cada paso para el incremento actual del vector de carga, formada por una carga específica.
Número de fases de carga. Esta opción permite al usuario configurar el número de pasos en los que la carga se cambia de cero a un valor especificado. En teoría, todas las soluciones se pueden encontrar dentro de un paso para el valor total de la carga de actuar. Sin embargo, surge la posibilidad de no unicidad de la solución, y, por otra parte, la solución encontrada pueden no tener significado físico. En tales casos, es razonable para especificar la carga incremental y obtener la solución no lineal para cada incremento. Desde el punto de vista computacional, a menudo es eficiente debido a que los efectos no lineales serán cada vez más pequeño en cada paso. Si los incrementos de carga son suficientemente pequeña en magnitud, cada solución incrementales se puede encontrar dentro de un paso con un alto grado de precisión. Por defecto, el número de pasos que se establece en 10.
Dirección actualización de carga permite al usuario para tener en cuenta el cambio en el vector de carga, mientras que la aplicación de la carga, de acuerdo con la geometría deformada del modelo.
Método de solución. Por defecto, se utiliza el método de Newton- Raphson para resolver el sistema de ecuaciones no lineales. En cada paso de aplicación de la carga, el sistema de las ecuaciones algebraicas lineales se está resolviendo hasta que el error relativo entre dos soluciones consecutivos no se convierte en menor que la tolerancia prescrita.
Si el número de iteraciones alcanza el valor más grande que el especificado, los cálculos se terminan.
Apéndice (Referencias)
Propiedades de los materiales estructurales
Una asignación adecuada de las propiedades del material utilizado en la estructura es un requisito previo importante para la corrección de análisis de elementos finitos. Las principales propiedades de los materiales estructurales utilizados para el análisis de la fuerza en AutoFEM son:
Módulo Elástico de un material E, [N/m2] -es la relación del esfuerzo con respecto a la tensión relativa ![]() el desarrollo en una muestra de una forma prismática son sometidos a una fuerza axial en un ensayo de tracción. En este caso, existe un estado de tensión uniforme en la mitad de la muestra en la dirección longitudal. El valor del Módulo Elástico E en el gráfico de la cepa
el desarrollo en una muestra de una forma prismática son sometidos a una fuerza axial en un ensayo de tracción. En este caso, existe un estado de tensión uniforme en la mitad de la muestra en la dirección longitudal. El valor del Módulo Elástico E en el gráfico de la cepa ![]() es numéricamente igual a la tangente del ángulo de inclinación del segmento lineal:
es numéricamente igual a la tangente del ángulo de inclinación del segmento lineal: ![]() en el gráfico de la tensión cuando se prueba una muestra. El sentido físico del módulo E se describe como la tensión requerida para la duplicación de la longitud de la muestra. Sin embargo, el valor de alargamiento elástico rara vez alcanza incluso 1% para la mayoría de los cuerpos sólidos.
en el gráfico de la tensión cuando se prueba una muestra. El sentido físico del módulo E se describe como la tensión requerida para la duplicación de la longitud de la muestra. Sin embargo, el valor de alargamiento elástico rara vez alcanza incluso 1% para la mayoría de los cuerpos sólidos.
El gráfico de la tensión de la espécimen probado tiene varios puntos especiales correspondientes a cambios en las propiedades físicas del material y se utiliza para evaluar el grado de fiabilidad de material bajo carga.
Elasticidad límite σп - el estrés que es el límite superior en el efecto de la cepa puramente elástica.
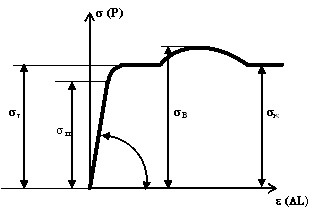
Diagrama de Estrés (dilatación) para materiales plásticos (por ejemplo, acero al carbono)
límite de Rendimiento σТ. Además de elongación de la muestra (por ejemplo, para aceros de bajo carbono) se produce prácticamente con ningún aumento en el fenómeno de carga. Este se llama "flujo plástico", y la parte horizontal del diagrama inmediatamente a la derecha desde el punto de curvatura se llama el rango de flujo plástico. En muchos materiales estructurales del margen de flujo plástico no es tan prominente visible, como en aceros de bajo carbono. La noción de límite elástico condicionalσ sse introduce para tales materiales, lo que es la tensión correspondiente a la (plástico) deformación residual igual a s%. en general, s = 0.2%. El límite de rendimiento para los materiales plásticos es seleccionado como el criterio de resistencia - la presión máxima de seguridad [sy]. Alcanzar tensiones correspondientes al límite de rendimiento provoca deformaciones plásticas irreversibles en la estructura, rompiendo así su viabilidad y es por lo tanto un comportamiento inadmisible desde el punto de vista de seguridad.
La mejor SR fuerza (resistencia reológico) es la tensión, al sobrepasar el cual se produce la ruptura del material. Tras un aumento en las cargas, hay un momento, después de lo cual más tensión se acumula en la muestra sin un aumento, o incluso en una reducción en, la carga, hasta la ruptura.
La relación de Poisson µ caracteriza desarrollo deformación transversal en una muestra de estiramiento. En la zona elástica, la deformación en la dirección transversal es ![]() , Donde ε - la tensión en la dirección longitudinal, µ— la relación de Poisson. Para materiales isótropos, la relación de Poisson se encuentra en el rango
, Donde ε - la tensión en la dirección longitudinal, µ— la relación de Poisson. Para materiales isótropos, la relación de Poisson se encuentra en el rango ![]() .
.
Por diversas calidades de acero, E = 195-206 GPa, µ = 0.23-0.31; para aleaciones de aluminio, E = 69-71 GPa, µ = 0.30-0.33.
Propiedades elásticas de algunos materiales se dan en la tabla (el denominador indica la propiedad de compresión respectiva).
Material |
Propiedades |
|
|
|
|
|
E, GPa |
σТ,MPa |
σE,,MPa |
δ, % |
ψ, % |
ST.3 |
200 |
240/240 |
450/- |
26 |
50 |
Acero 15 |
200 |
210/210 |
350/- |
28 |
55 |
Acero 45 |
200 |
340/340 |
610/- |
24 |
45 |
Acero 30HGSA |
200 |
950/950 |
1200/- |
13 |
- |
hierro fundido S-Ch-15-32 |
150 |
- |
150/640 |
0,6 |
45 |
Alambre de cobre |
110 |
250/250 |
320/- |
15 |
- |
Duraluminio D16 |
75 |
240/240 |
420/- |
18 |
- |
Madera Delta (madera contrachapada) |
20 |
- |
250/160 |
- |
- |
Textolite |
30 |
75/115 |
127/168 |
1,5 |
- |
Propiedades de plasticidad de un material son el alargamiento relativo y contracción relativa a la rotura:
![]() ,
, ![]()
Donde l0, F0 -
la longitud de la parte de trabajo de la muestra y del área de la sección transversal antes de cepa; lk - la longitud de la parte de trabajo de la muestra después de la ruptura; Fk - la última área de la sección transversal en el cuello de la muestra después de la ruptura.
Los estados de plástico y material quebradizo se distinguen por la cantidad de alargamiento relativo a la rotura. Materiales en desarrollo valores suficientemente altos ![]() en el punto de ruptura se refiere a materiales como plástico, los mencionados como frágiles son los materiales con el alargamiento relativo de
en el punto de ruptura se refiere a materiales como plástico, los mencionados como frágiles son los materiales con el alargamiento relativo de ![]() .Para los materiales de plástico, a la compresión a cerca de la condición de rendimiento, la
.Para los materiales de plástico, a la compresión a cerca de la condición de rendimiento, la ![]() patrón gráfico es el mismo que en el caso de la tensión. En virtud de un esfuerzo de compresión, el espécimen se acorta, mientras tanto, sus dimensiones de la sección transversal crecen. Para ciertos materiales de plástico, es imposible encontrar la tensión análoga a la tracción resistencia reológico debido al aplanamiento de la muestra.
patrón gráfico es el mismo que en el caso de la tensión. En virtud de un esfuerzo de compresión, el espécimen se acorta, mientras tanto, sus dimensiones de la sección transversal crecen. Para ciertos materiales de plástico, es imposible encontrar la tensión análoga a la tracción resistencia reológico debido al aplanamiento de la muestra.
Los materiales frágiles exhiben mucho mejor capacidad para resistir la deformación por compresión, en lugar de la tensión de dilatación; para aquellos, la cepa ruptura de compresión excede la resistencia última a la tracción múltiple. La rotura de materiales quebradizos bajo compresión se produce debido a la formación de grietas.
Volumen Estado esfuerzo-deformación en un punto
El estado deformado en un punto de un cuerpo deformable se describe por el tensor de deformación simétrica:
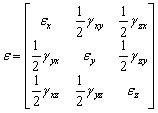 ,
,
Donde ![]() - la deformación longitudinal relativa,
- la deformación longitudinal relativa, ![]() ,
, ![]() ,
, ![]() - la deformación angular. Siempre se puede especificar las tres direcciones ortogonales, de modo que los ángulos escarpados son todos ceros, mientras que los alargamientos son
- la deformación angular. Siempre se puede especificar las tres direcciones ortogonales, de modo que los ángulos escarpados son todos ceros, mientras que los alargamientos son![]() . las deformaciones
. las deformaciones ![]() ,
, ![]() ,
, ![]() en las direcciones, por lo que los ángulos escarpados están ausentes, se llaman las tensiones principales en un punto.
en las direcciones, por lo que los ángulos escarpados están ausentes, se llaman las tensiones principales en un punto.
Juntos, los nueve componentes de estrés (por tres por cada uno de los quilates mutuamente perpendiculares) constituyen una entidad física llamada, tensor de tensiones en un punto. El tensor se representa por una matriz simétrica:
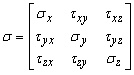 ,
,
Donde ![]() - el esfuerzo de compresión-tensión,
- el esfuerzo de compresión-tensión, ![]() ,
, ![]() ,
,![]() , - el esfuerzo cortante.
, - el esfuerzo cortante.
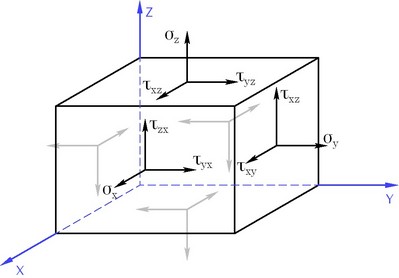
Las componentes del tensor del estado de estrés en un bloque infinitesimal
La siguiente regla de los signos se utiliza comúnmente para componentes del tensor tensión: un componente es positivo, si apunta en la dirección positiva del respectivo eje de coordenadas de un quilate con lo positivo normales externo alineado con una de las coordenadas.
Tanto el tensor de tensiones y el tensor de deformaciones poseen la propiedad de simetría. ![]() ,
, ![]() ,
,![]() . Las condiciones de simetría del tensor de tensiones también se conocen como emparejado pura tensiones condiciones: las tensiones escarpados que actúan sobre dos quilates perpendiculares entre sí en las direcciones ortogonales al borde en la intersección de esos quilates son iguales en magnitud. Debido a estas propiedades, de los nueve componentes del tensor de tensiones son seis los independientes.
. Las condiciones de simetría del tensor de tensiones también se conocen como emparejado pura tensiones condiciones: las tensiones escarpados que actúan sobre dos quilates perpendiculares entre sí en las direcciones ortogonales al borde en la intersección de esos quilates son iguales en magnitud. Debido a estas propiedades, de los nueve componentes del tensor de tensiones son seis los independientes.
Al igual que en el caso de la cepa, el concepto de tensiones principales se introduce en un estado de estrés, ![]() , correspondiente a las cepas principales, relacionados con los componentes del tensor de estrés por la ecuación:
, correspondiente a las cepas principales, relacionados con los componentes del tensor de estrés por la ecuación:
![]() , Donde;
, Donde;
![]() ,
,  ,
, 
Una solución ecuación cúbica tiene tres raíces reales ![]() , los cuales están comúnmente clasificadas de la siguiente manera:
, los cuales están comúnmente clasificadas de la siguiente manera: ![]() .Los esfuerzos principales poseen una propiedad importante: las tensiones normales en las principales quilates de dirección orientada son más altas entre los de cualquier otro quilates. También introdujo el concepto de tensión media mediante la fórmula
.Los esfuerzos principales poseen una propiedad importante: las tensiones normales en las principales quilates de dirección orientada son más altas entre los de cualquier otro quilates. También introdujo el concepto de tensión media mediante la fórmula
![]()
Evaluación de la fuerza estática de la estructura. Teorías fuerza
El último estado de tensión segura es cuando las propiedades del material se someten a un cambio cualitativo - una transición de un estado mecánico a otro. Para los materiales de plástico, el estado de deformación seguro es considerado comúnmente como el estado de desarrollo de la tensión residual notable, mientras que para los más frágiles - una condición cuando un material comienza a agrietarse. El estado final no es admisible para los materiales. Por lo tanto, cuando se realiza el análisis de la fuerza, seguir el llamado Estado admisible. Se corresponde con la carga obtenida dividiendo la carga del estado último-fuerza por un factor de seguridad. Si los factores de seguridad son iguales en dos estados de estrés, que los que están llamados igualmente a prueba de fallos. Para comparar los diferentes estados tensas, el simple tensión (compresión) es aceptada como la medida universal, con la tensión principal ![]() .
.
Estrés equivalente ![]() - El estrés que se desarrollarán en un espécimen estirado para hacer su estado igualmente inseguro como un estado de tensión especificado. El criterio de resistencia se escribe como
- El estrés que se desarrollarán en un espécimen estirado para hacer su estado igualmente inseguro como un estado de tensión especificado. El criterio de resistencia se escribe como ![]() .
.
Teorías de fuerza son las hipótesis acerca de los criterios que describen las condiciones de un material de alcanzar el estado de resistencia última.
Teoría Primera fuerza
En la primera teoría de la fuerza, la resistencia a la rotura de un material se refiere a la tensión máxima normal. De acuerdo con esta teoría, el estado inseguro se produce cuando uno de los esfuerzos principales alcanza un umbral de seguridad. De acuerdo con ello, la magnitud de las tensiones principales máxima está limitada a fin de no exceder la tensión principal máxima ![]() . El criterio de resistencia aparece como:
. El criterio de resistencia aparece como: ![]() , Donde
, Donde ![]() , if
, if ![]() y
y ![]() , if
, if ![]() .
.
Teoría Segunda fuerza
La segunda teoría fortaleza utiliza la tensión máxima que el criterio de resistencia última. De acuerdo con esta teoría, el estado inseguro de un material se produce cuando la cepa lineal alcanza un cierto umbral de seguridad. Para un material de plástico, el criterio de resistencia aparece como ![]() , donde
, donde ![]() .Si, por ejemplo,
.Si, por ejemplo, ![]() , entonces
, entonces ![]() .
.
Para materiales frágiles, aparece el criterio de resistencia como:
![]() ,
, ![]()
La primera teoría se obtiene buen acuerdo con los datos experimentales sólo para materiales frágiles. El segundo está prácticamente abandonado en la actualidad.
Teoría Tercera fuerza
En la teoría de la tercera fuerza, la resistencia a la rotura se refiere a la tensión máxima pura. De acuerdo con esta teoría, el estado inseguro se produce cuando la tensión máxima pura alcanza un umbral de seguridad.
El criterio de resistencia aparece como: ![]() , donde
, donde ![]() .consecuentemente:
.consecuentemente: ![]()
Cuarto (energía) Teoría fuerza
La cuarta teoría de fuerza se basa en el enfoque de la energía, sobre la base de la hipótesis de que la causa de un estado inseguro es la magnitud de la densidad de energía potencial de uф deformación, por lo tanto, el criterio se refiere a la densidad de la energía potencial de la deformación.
Vamos a derivar la fórmula para la densidad de energía potencial debido a la distorsión de la fórmula para la densidad de energía potencial completo debido a la tensión, mediante el uso de la relación de Poisson específica de μ = 0,5.
Que los rendimientos:
![]()
El criterio de resistencia aparece como ![]() , donde
, donde ![]() .
.
En consecuencia:
![]()
o
![]()
La tercera y cuarta teorías de fuerza producen acuerdo satisfactorio de los resultados de cálculos teóricos con los datos de pruebas de laboratorio para materiales plásticos y son ampliamente utilizados en el análisis de la fuerza. Estas teorías no son aplicables para materiales frágiles.