 |
AutoFEM Analysis Análisis de Fatiga | ||||||
Análisis de fatiga
Algunas partes de máquinas, mecanismos, así como elementos arquitectónicos en el proceso de operación están sometidos a cargas que varían con el tiempo. Análisis de estrés de los problemas con este tipo de carga difiere del análisis de las cargas estáticas y de impacto. El módulo de análisis de fatiga de la AutoFEM Analysis se utiliza para el estudio de la fuerza de diseño bajo la acción de cargas variables. La fatiga es un proceso de acumulación gradual de daños en el material bajo la influencia de las variables de estrés, lo que lleva a la formación de grietas, su desarrollo y la eventual destrucción de la estructura.
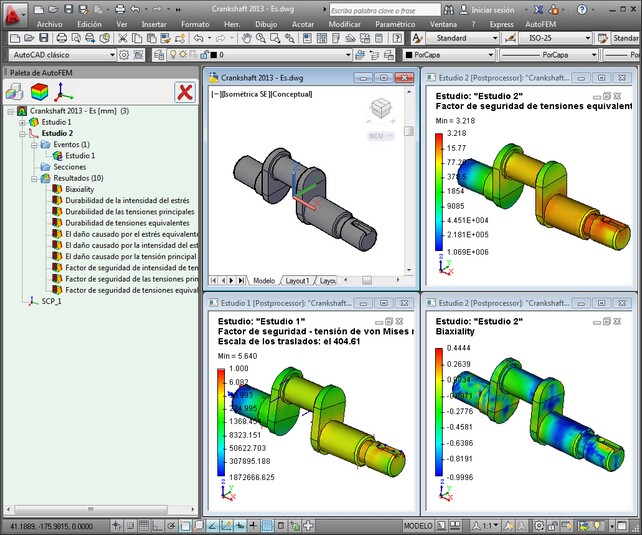
Detalles de fatiga pasos de análisis
Antes de realizar el cálculo de la resistencia, usted primero debe explorar el efecto de la carga estática en el elemento o estructura determinada (es decir, realizar un análisis estático). Esto es necesario con el fin de determinar si una falla del producto bajo una carga estática dada. Si el diseño se destruye a una carga estática dada (el factor de seguridad menor que 1), a continuación, realizar un análisis de la fatiga no tiene sentido.
Un problema preliminar cálculo de análisis estático es necesario también porque el análisis de tensión estática calculada (director o equivalente) se utiliza para calcular la resistencia a la fatiga como la amplitud de esfuerzos cíclicos.
Además para el análisis de la fatiga es necesario que curva SN se ha determinado para el material del que está fabricado el producto. Crear el problema de analizar la fatiga.
Puede utilizar una de las siguientes formas de crear estudio:
Linea de comando: |
_FEMASTUDY |
Menú principal: |
AutoFEM | Crear un estudio... |
Icono: |
|
Luego hay que especificar el tipo de estudio ("Análisis de la fatiga") en la ventana de propiedades.
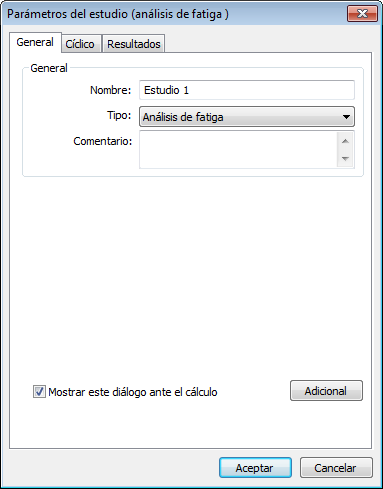
Para la creación del ciclo de fatiga que usted tiene que:
| 1. | Invocar la ventana de propiedades del ciclo de fatiga por la elección de los grupos de "Eventos" en el gestor de estudios en la ventana "AutoFEM Palette" y llevar a cabo el comando "Add..." en el menú contextual (presionando |
| 2. | Añadir estudio estático que debe ser ya aplicado. |
| 3. | Establecer parámetros del ciclo de fatiga: el número de ciclos, relación de esfuerzos, factor de escala. |
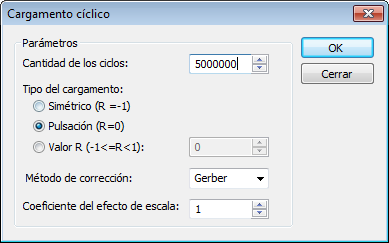
Es posible llevar a cabo análisis de fatiga para varios eventos de diferentes estudios estáticos. Por ejemplo, si dos o más fuerzas son cíclicos, pero por que tener una ley diferente de variar. Cabe señalar que el elemento finito mallas de tesis estudios estáticos deben ser idénticos y el mismo cuerpo de cada estudio debe tener el mismo material.
También puede establecer "factor de concentración de esfuerzos" en la ficha "fatiga" de las "Propiedades de estudio (análisis de fatiga)" de diálogo (por defecto es igual a 1).
Los resultados del análisis de la fatiga.
Después de realizar el cálculo de una nueva carpeta ("Resultados") se crea en el árbol de estudio. Usted puede especificar la lista de resultados que se muestran en la pestaña "Resultados" de las "Propiedades de estudio (análisis de fatiga)" de diálogo.
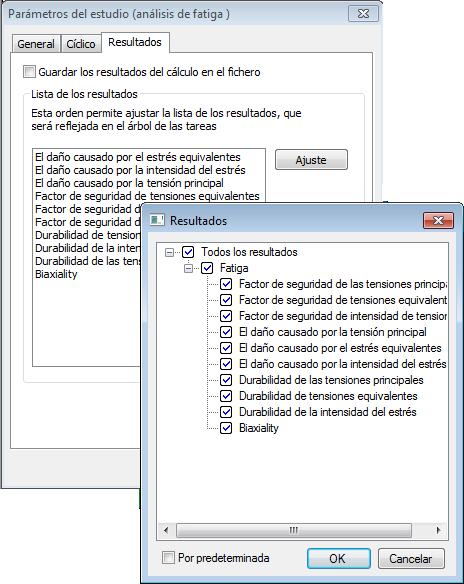
En todos los diez resultados están disponibles para el análisis de fatiga. Se pueden dividir en cuatro grupos.
Grupo " Daño " incluye los siguientes resultados:
| • | Daños por tensiones principales (hipótesis 3); |
| • | Daños por tensiones equivalentes (hipótesis 2); |
| • | Daños por la intensidad del estrés (hipótesis 1); |
Este resultado se muestra en porcentaje y se indica la tasa de daños de la estructura bajo la acción de esfuerzos cíclicos en una el número y la naturaleza de los ciclos de carga especificada.
Si el diseño presentado a n1 ciclos de tensión alternaS1, n2 ciclos de tensión alterna S2, n3 ciclos de tensión alterna S3,..., nk ciclos de tensión alterna Sk, entonces la tasa de daño total D se calcula como: D = n1 / N1 + n2/N2 + n3/N3![]() +...+ nk/Nk, where Ni es el número de ciclos requerido para causar la destrucción por Si.
+...+ nk/Nk, where Ni es el número de ciclos requerido para causar la destrucción por Si.
Grupo "Vida Total" (este tipo de resultado sólo está disponible para un solo caso de estudio el análisis de fatiga) incluye los siguientes resultados:
| • | De vida total por tensiones principales; |
| • | De vida total por tensiones equivalentes; |
| • | La vida total de intensidad de tensiones. |
Este resultado muestra el número mínimo de ciclos de Nmin, requerida para provocar el fallo por fatiga.
Grupo "factor de seguridad" (este tipo de resultado sólo está disponible para el evento único estudio de análisis de fatiga) incluye los resultados:
| • | factor de seguridad por las tensiones principales máximas (hipótesis 3). |
| • | factor de seguridad por tensiones equivalentes (hipótesis 2); |
| • | factor de seguridad de intensidad de tensiones (hipótesis 1); |
El factor de seguridad es la relación entre límite de fatiga σR, definedpara una curva de fatiga dado para un número dado de ciclos de carga, ajustada a la amplitud del ciclo σ*,que se calcula a partir de los cálculos en el problema de análisis de tensión estática σ:
![]()
Las tensiones σ se calculan sobre la base de las condiciones pertinentes de la plasticidad:
la distorsión hipótesis de energía:
![]() ;
;
| • | La hipótesis de tensiones tangenciales máximas: |
| • | El más grande director hipótesis del estrés: |
Grupo "biaxialidad" (este tipo de resultado sólo está disponible para el evento único estudio de análisis de fatiga) incluye el siguiente resultado:
Biaxialidad es la relación de la tensión principal más pequeña alterna (diferente de 0) a una tensión principal mayor alterna:
![]() .
.
Este resultado caracteriza a la desigualdad de las amplitudes de las tensiones principales en el punto y describe la distribución espacial de la irregularidad de los esfuerzos principales en el volumen del cuerpo en cada punto. El valor de la biaxialidad igual a 1 corresponde al caso de estado igual estrés σ1=σ2=σ3 en el punto.
Apéndice (Referencias)
El ciclo de estrés. Las propiedades generales
Después de un cierto número de cargas repetidas (o ciclos de tensión) la destrucción final de las piezas puede ocurrir, por otra parte, es posible que la destrucción no tiene lugar bajo constante estrés load.The número de ciclos de tensión hasta que la fractura depende la magnitud (amplitud de la tensión) y varía en un amplio intervalo. Por destruir bajo altas tensiones 5-10 ciclos son suficientes, por otro lado, bajo tensiones inferiores detalle soportar millones o miles de millones de ciclos, y bajo incluso menos tensiones que es capaz de funcionar indefinidamente.
Hay máxima σmaxy mínimo σmin ciclos de esfuerzo que permitan entender el más grande y el más pequeño del valor algebraica del ciclo de estrés. Como medio de estrés σm y la amplitud σa de la toma ciclo de estrés: σm= ( σmax + σmin ) / 2, σa= ( σmax - σmin ) / 2. Escala de estrés se llama la diferencia entre el máximo y el mínimo estrés cycle, i.e. 2σa= ( σmax - σmin ).
El ciclo en el que el máximo y el mínimo estrés en valor absoluto son diferentes, llama asimétrica.
Un caso especial del ciclo asimétrico está pulsando ciclo en el que el ciclo de estrés mínimo es cero: σmin = 0.
Simétrico es un ciclo en el que las tensiones máximas y mínimas son iguales en magnitud pero de signo opuesto.
Para caracterizar el grado de asimetría de la tensión se utiliza la relación asimétrica de estrés, que es la relación de mínimo a máximo de ciclo de estrés: R=σmin/σmax.
Tipo de ciclo de estrés: |
Asimétrico |
Pulsante |
Simétrico |
Relación de esfuerzos R=σmin/σmax : |
R1 |
0 |
-1 |
Tensión mínima σmin : |
R1*σmax |
0 |
- σmax |
Esfuerzo máximo σmax : |
σmax |
σmax |
σmax |
La media de estrés σm : |
(1 + R1 )*σmax/2 |
σmax/2 |
0 |
Rango de tensiónσa : |
(1 - R1 )*σmax/2 |
σmax/2 |
σmax |
Gama estrés 2σa : |
(1 - R1 )*σmax |
σmax/2 |
2*σmax |
|
|
|
||
ciclo asimétrico ( R= - 0.2) |
ciclo simétrico ( R= -1 ) |
ciclo pulsante ( R= 0 ) |
Los métodos de corrección de la tensión
Deje que σ* se corrige la tensión alterna, σY es el límite elástico, σT es resistencia a la tracción, a continuación:
| 1. | Método de Soderberg σ* = σa / ( 1 - σm / σY ) |
| 2. | Método de Goodman se utiliza para materiales frágiles: σ* = σa / ( 1 - σm / σT ) |
| 3. | Método de Gerber se utiliza para materiales plásticos: σ* = σa / ( 1 - ( σm / σT )2 ) |
Evaluación de las características de resistencia a la fatiga bajo estado de tensión compleja
Condiciones de fuerza con la alternancia de las tensiones en términos generales similares a las condiciones de resistencia de análisis estático, sino como la tensión máxima admisible utilizada límite de fatiga σR. En consecuencia, el criterio prueba de hipótesis resistencia a la fatiga para evitar la deformación plástica en los cálculos de fatiga adoptan la forma σ* ≤ σR ![]() . Recordamos las expresiones generales de prueba de hipótesis tradicional de fuerza (para la condición de plasticidad), utilizado para evaluar la resistencia de las estructuras:
. Recordamos las expresiones generales de prueba de hipótesis tradicional de fuerza (para la condición de plasticidad), utilizado para evaluar la resistencia de las estructuras:
| 1. | Tresca - Saint-Venant hipótesis (la hipótesis del esfuerzo cortante máximo) σY < ( σ1 - σ3 ), | σ1 | ≥ | σ2 | ≥ | σ3 | |
| 2. | Huber - Mises hipótesis (hipótesis de la energía de distorsión) |
| 3. | Mohr hipótesis (hipótesis de la mayor tensión principal) σY < σ1 , | σ1 | ≥ | σ2 | ≥ | σ3 | |
Donde; ![]() σY es la tensión de fluencia, σ1 , σ2 , σ3 son las tensiones principales. Por lo tanto, al analizar la fatiga, también obtenemos tres opciones para el factor de seguridad correspondiente a cada uno de la teoría generalmente aceptada de la resistencia del material.
σY es la tensión de fluencia, σ1 , σ2 , σ3 son las tensiones principales. Por lo tanto, al analizar la fatiga, también obtenemos tres opciones para el factor de seguridad correspondiente a cada uno de la teoría generalmente aceptada de la resistencia del material.