Language

AutoFEM Analysis es un sistema de análisis de elementos finitos.
La principal característica del sistema es su profunda integración con AutoCAD

Con AutoFEM los usuarios de AutoCAD pueden resolver el problema de la modelización por elementos finitos de los varios fenómenos físicos:

Algoritmo general del trabajo con AutoFEM es la siguiente:
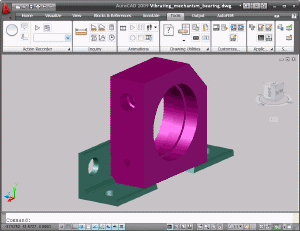
En primer lugar, el usuario crea un modelo tridimensional (3D) del producto en el entorno de AutoCAD 3D.

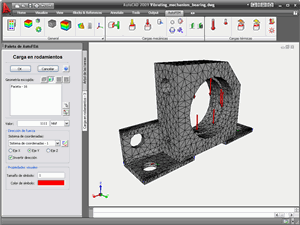
Luego, sin salir de AutoCAD, se crea un problema de análisis de elementos finitos, llamado la «estudio». El modelo se carga en el Pre-procesador de AutoFEM, integrado en AutoCAD. Usando el Pre-procesador el usuario especifica los parámetros internos y externos de los fenómenos de simulación física (malla de elementos finitos, las condiciones de frontera, materiales, etc) y transmite «estudio» en el Procesador de AutoFEM.

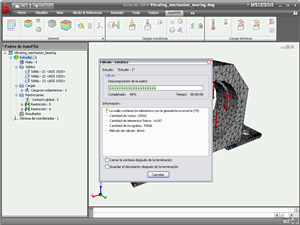
Procesador de AutoFEM realiza la construcción y la solución de las sistemas de los ecuaciones algebraicas, de conformidad con el método del elementos finitos.

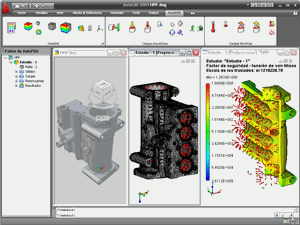
En usuario postprocesador la AutoFEM realiza un análisis de los resultados y la formación de los documentos de acompañamiento - informes, vídeo, avi, etc

Así, los usuarios de AutoCAD que poseen, tienen la oportunidad de llevar a cabo la simulación de elementos finitos en el habitual y familiar del entorno de software.

Descargar vídeo de demostración sobre AutoFEM Análisis

Teórica de fondo de AutoFEM Análisis

AutoFEM Análisis - es un software de análisis de elementos finitos, basado en el método de elementos finitos.
Método de Elementos Finitos (MEF) es la vía que conduce a predecir el comportamiento de las estructuras en condiciones reales.
El principio general del método de elementos finitos es la siguiente.
El diseño, que es, en general, un sistema con un número infinito de grados de libertad, se divide en un número finito de volúmenes elementales - los elementos finitos llamada. Como la forma de un elemento finito se conoce de antemano (segmento de línea, triángulo, caja, etc) es posible escribir las relaciones que establecen una relación matemática entre las variaciones de una magnitud física en un solo elemento.
Por ejemplo, para el problema de análisis de resistencia estática se determina la dependencia de la forma geométrica de un elemento finito (cepa) del elemento agregado a las fuerzas externas. la forma geométrica de un elemento finito es definida por las coordenadas espaciales de puntos específicos en los límites de uno de los elementos finitos, que se llaman nodos. Aplicación a las fuerzas de los elementos finitos provoca un desplazamiento de nodos (cepa). Este cambio se puede expresar en forma de ecuaciones algebraicas. Para el análisis térmico determina la dependencia de la distribución de temperaturas en términos de elementos finitos.
Para cada uno de los elementos finitos se construye un sistema de ecuaciones algebraicas que describen la formulación matemática del problema físico. Por ejemplo, para el problema de la resistencia estática en la forma de la matriz del sistema de ecuaciones se puede escribir como
[Kel] * [Xel] = [Pel], donde
[Kel] - matriz de rigidez de los elementos finitos
[Pel] - vector de fuerzas aplicadas a los elementos finitos
[Xel] - el vector de desplazamientos en los puntos característicos del elemento finito, llamado nodos. Este vector se va a determinar.
En la primera versión AutoFEM Análisis de elementos finitos como utilizar tetraedro. Tetraedro puede aproximar la geometría de arbitrariedad compleja del objeto real simulado. Un generador especial de las mallas de elementos finitos tetraédricos crea una malla de elementos finitos para el modelo sólido tridimensional de un producto fabricado en AutoCAD.
Después de construir la malla de elementos finitos y el cálculo de matrices de rigidez local de cada elemento finito es posible algebraica y topológicamente resumir todos los elementos de la rigidez de la matriz y locales para construir la matriz de rigidez global de la asamblea. El resultado (por ejemplo, el análisis estático) es un sistema de ecuaciones de la forma

[KGL] * [XGL] = [PGL], donde

[KGL] - matriz de rigidez global de la construcción.
[PGL] - el vector global de fuerzas externas.
[XG] - que se determinarán el vector de desplazamientos nodales desconocidos.
Procesador de AutoFEM Analysis realiza la generación de la matriz de rigidez global y la solución de ecuaciones algebraicas. Existen algunos métodos para resolver ecuaciones algebraicas. Uno de los más famosos y utilizados es el método de Gauss (o de sus modificaciones como el método de Cholesky). Estos métodos suelen ser llamados como métodos directos de solución de ecuaciones algebraicas. El segundo grupo grande de los métodos de álgebra lineal para resolver ecuaciones algebraicas son los métodos iterativos de resolución de ecuaciones algebraicas como el método de gradiente conjugado.
Procesador de AutoFEM análisis utiliza dos métodos de estos grupos para la resolución de ecuaciones algebraicas lineales y no lineales que son considerados en la modelización de elementos finitos.
Después de resolver las ecuaciones en cada nodo de la malla de elementos finitos se conoce el desplazamiento y el estrés (por la estática), u otras cantidades físicas como la temperatura para el análisis térmico. Estos datos se transmiten en Postprocesador AutoFEM de análisis, que se ha integrado plenamente en la interfaz de AutoCAD.
La teoría del método de elementos finitos se describe en muchos libros y artículos. No es fácil recomendar cualquiera de ellos, porque las cantidades no se trata de cientos de miles de personas. Posiblemente uno de los autores más famosos sobre el tema FEM es OC Zienkiewicz. Sus libros han sido traducidos a todas las lenguas europeas. Por ejemplo, uno de la última edición de su libro es Zienkiewicz OC, Taylor RL vol. 1-3. El método de elementos finitos. (2000) (T).
Análisis AutoFEM utiliza diferentes algoritmos de elementos finitos que se describen en los artículos científicos y libros especializados en temáticas y análisis de elementos finitos FEM.