 |
AutoFEM Analysis Analyse de fatigue | ||||||
Analyse de fatigue
Certains éléments de machines, des mécanismes, ainsi que des éléments d'architecture sont soumises à des charges qui varient avec le temps. L'analyse de fatigue avec de telles charges diffère de l'analyse pour les charges statiques. Le module d'analyse de la fatigue d'AutoFEM est utilisé pour l'étude de la résistance de structures sous l'action de charges variables. La fatigue est un processus d'accumulation progressive de dégâts dans le matériel sous l'influence de stress variable, conduisant à la formation de fissures, de leur développement et la destruction éventuelle de la structure.
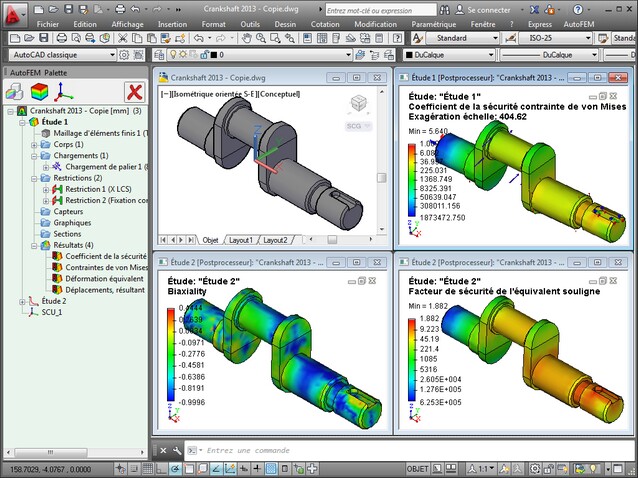
Détails des étapes de l'analyse de fatigue
Avant d'effectuer le calcul de fatigue, il faut d'abord explorer l'effet de la charge statique sur la structure (par exemple effectuer une analyse statique). Ceci est nécessaire afin de déterminer si une défaillance du produit sous une charge statique donnée se produit. Si l'objet est déjà détruit avec une charge statique (le facteur de sécurité inférieur à 1), effectuer une analyse de fatigue n'a pas de sens.
Une analyse statique préliminaire est nécessaire aussi parce que la contrainte statique calculée (principale ou équivalente) sera utilisé pour calculer la résistance à la fatigue comme l'amplitude des contraintes cycliques.
En outre, pour l'analyse de fatigue, il est nécessaire que la courbe S-N aie été déterminée pour le matériel à partir duquel le produit est fabriqué.
Créer le problème de l'analyse fatigue.
Vous pouvez utiliser l'une des façons suivantes pour créer l'étude:
Commande: |
_FEMASTUDY |
Menu principal: |
AutoFEM | Créer une étude... |
Icône: |
|
Ensuite, vous devez spécifier le type de l'étude («analyse de fatigue") dans la fenêtre des propriétés.
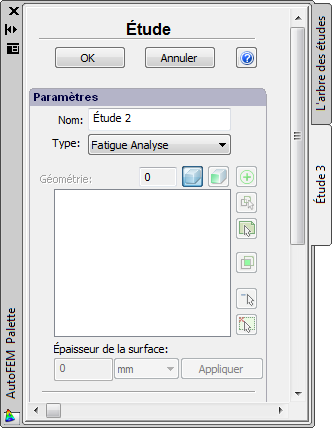
Pour créer le cycle de fatigue, vous devez:
| 1. | Ouvrez la fenêtre de propriétés du cycle de fatigue en choisissant le groupe "Événements" de l'arbre des études dans la fenêtre "AutoFEM Palette» et d'exécuter la commande "Ajouter ..." du menu contextuel (en appuyant |
| 2. | Ajouter l'étude statique qui a déjà été calculée. |
| 3. | Définissez les paramètres du cycle fatigue: la quantité de cycles, le taux de stress et le facteur d'échelle. |
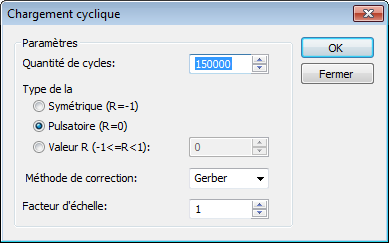
Il est possible d'effectuer une analyse de fatigue pour plusieurs événements de différentes études statiques. Par exemple, si deux ou plusieurs forces sont cycliques mais ils ont de différente lois de variations. Il faut remarquer que les maillages d'éléments finis d'études statiques doivent être identiques, et tous les corps de chaque étude doivent avoir le même matériel.
Vous pouvez également définir «facteur de concentration de contrainte" dans l'onglet "fatigue" de la boîte de dialogue "Propriétés de l'étude" (par défaut, il est égal à 1).
Les résultats de l'analyse de fatigue
Après avoir effectué le calcul un nouveau dossier («Résultats») est créé dans l'arbre de l'étude. Vous pouvez spécifier la liste des résultats affichés dans l'onglet "Résultats" de la boîte de dialogue "Propriétés de l'étude".
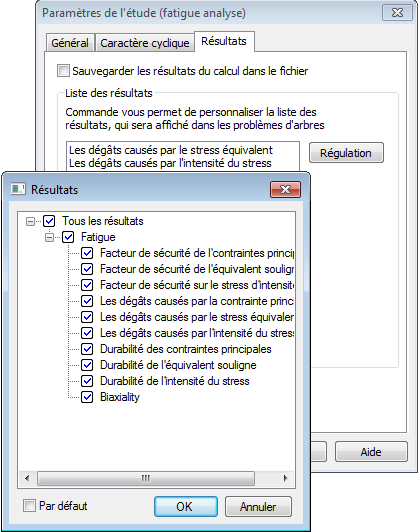
En tout, dix résultats sont disponibles pour l'analyse de la fatigue. Ils peuvent être divisés en quatre groupes:
Groupe «Dommage» inclut les résultats suivants:
| • | dommages causés par les contraintes principales (hypothèse 3); |
| • | dommages causés par les contraintes équivalentes (hypothèse 2); |
| • | dommages causés par l'intensité du stress (hypothèse 1); |
Ce résultat est affiché en pourcentage et indique le taux de dommage de la structure sous l'action de contraintes cycliques à une indication du nombre et de la nature des cycles de charge.
Si l'objet soumis à n1 cycles de contraintes équivalentes S1, n2 cycles de contraintes équivalentes S2, n3 cycles de contraintes équivalentes S3, ..., nk cycles de contraintes équivalentes Sk, le taux total D de dommages est calculé comme suit: D = n1 / N1 + n2/N2 + n3/N3+...+ nk/Nk , ou Ni est le nombre de cycles nécessaire pour provoquer la destruction par Si.
Groupe "durée de vie" (ce type de résultat n'est disponible que pour l'étude de l'analyse de fatigue avec événement isolé) comprend les résultats suivants:
| • | durée de vie totale par contraintes principales; |
| • | durée de vie totale par contraintes équivalentes; |
| • | durée de vie totale par l'intensité du stress. |
Ce résultat indique le nombre minimum de cycles Nmin, nécessaire pour provoquer la rupture par fatigue.
Groupe «Facteur de sécurité" (ce type de résultat n'est disponible que pour l'étude de l'analyse de fatigue avec événement isolé) comprend les résultats:
| • | facteur de sécurité par contraintes principales maximales (hypothèse 3). |
| • | facteur de sécurité par contraintes équivalentes (hypothèse 2); |
| • | facteur de sécurité par l'intensité du stress (hypothèse 1); |
Le facteur de sécurité est le rapport de la limite de fatigue σR, défini par la courbe de fatigue pour un certain nombre de cycles de chargement, ajusté à l'amplitude du cycle σ*,qui est calculé à partir des du problème de l'analyse des contraintes statiques σ:
![]()
les contraintes σ sont calculées sur la base des conditions pertinentes de plasticité:
| • | l'hypothèse de l'énergie de distorsion |
| • | l'hypothèse du cisaillement maximal |
| • | l'hypothèse du la contrainte principale la plus grande: |
Groupe "Biaxialité" (ce type de résultat n'est disponible que pour l'étude de l'analyse de fatigue avec événement isolé) et comprend le résultat suivant.
La biaxialité est le rapport de la plus petite contrainte principale alternative (différente de 0) à une plus grande contrainte principale en alternance:
![]() .
.
Ce résultat caractérise l'inégalité des amplitudes des contraintes principales à ce point et décrit la distribution spatiale des irrégularités des contraintes principales sur le volume du corps en tous points. La valeur de la biaxialité égale à 1 correspond au cas de l'état de contrainte égal σ1=σ2=σ3 à ce point
Annexe (références)
Le cycle de contrainte. Les propriétés générales
Après un certain nombre de charges répétées (ou cycles de stress) la destruction finale de l'objet peut se produire. D'autre part, il est possible que la destruction n'ai pas lieu sous ce nombre de charges. Le stress constant de cycles de contraintes jusqu'à la fracture dépend de l'amplitude (de la contrainte) et varie sur une large gamme. Pour la destruction sous de fortes contraintes 5-10 cycles suffisent, d'autre part, soumis à des contraintes plus faibles des millions ou des milliards de cycles peuvent être supportés, et sous encore moins de contraintes, il est capable de fonctionner indéfiniment.
Il y a le maximum σmax et le minimum σmin de cycles de stress permettant de comprendre la plus grande et la plus petite valeur algébrique du cycle de stress. Comme moyenne de stress σm et amplitude σa du cycle de stress: σm= ( σmax + σmin ) / 2 , σa= ( σmax - σmin ) / 2. La différence entre le maximum et le minimum du cycle stress est appelé échelle de stress , ex. 2σa= ( σmax - σmin ).
Le cycle dans lequel la valeur maximale et minimale de stress en valeur absolue sont différentes, est appelé asymétrique.
Un cas particulier du cycle asymétrique est le cycle pulsatoire auquel le stress minimale est égale à zéro: σmin = 0.
Symétrique est un cycle dans lequel le stress maximal et minimal sont égaux en grandeur absolus mais de signe opposé.
Pour caractériser le degré d'asymétrie de stress le rapport de stress asymétrique, qui est le rapport du minimum au maximum du cycle de stress, est utilisé, : R=σmin/σmax .
Type de cycle de stress : |
asymétrique |
pulsatoire |
symétrique |
Le rapport de stress R=σmin/σmax : |
R1 |
0 |
-1 |
Stress minimum σmin : |
R1*σmax |
0 |
- σmax |
Stress maximum σmax : |
σmax |
σmax |
σmax |
contrainte moyenne σm : |
(1 + R1 )*σmax/2 |
σmax/2 |
0 |
Gamme de stress σa : |
(1 - R1 )*σmax/2 |
σmax/2 |
σmax |
l'étendue de stress 2σa : |
(1 - R1 )*σmax |
σmax/2 |
2*σmax |
|
|
|
||
cycle asymétrique ( R= - 0.2) |
cycle symétrique ( R= -1 ) |
cycle pulsatoire ( R= 0 ) |
Méthodes de correction du stress
σ* est le stress altérnant σY est la charge σT est résistance à la traction, alors:
| 1. | Méthode Soderberg σ* = σa / ( 1 - σm / σY ) |
| 2. | Méthode Goodman pour matériaux friables σ* = σa / ( 1 - σm / σT ) |
| 3. | Méthode Gerber pour matériaux plastiques : σ* = σa / ( 1 - ( σm / σT )2 ) |
Évaluation des caractéristiques de résistance à la fatigue sous l'état de stress complexe
Les forces de résistance au stress alternées sont en général semblables aux forces d'analyse statique, mais la fatigue limite est utilisée en tant que stress maximal admissible σR . En conséquence, le test d'hypothèse pour le critère de résistance à la fatigue pour éviter la déformation plastique dans les calculs de fatigue prennent la forme σ* ≤ σR . Nous rappelons les expressions générales du test d'hypothèse traditionnelle de force (pour les conditions de plasticité), utilisés pour évaluer la résistance des structures:
| 1. | L'hypothèse Tresca - Saint-Venant (l'hypothèse de la contrainte de cisaillement maximale) σY < ( σ1 - σ3 ), | σ1 | ≥ | σ2 | ≥ | σ3 | |
| 2. | L'hypothèse Huber - Mises hypothesis (hypothèse de l'énergie distorsion) |
| 3. | L'hypothèse Mohr (l'hypothèse la plus grande contrainte principale) σY < σ1 , | σ1 | ≥ | σ2 | ≥ | σ3 | |
ou σY est la limite d'élasticité, et σ1 , σ2 , σ3 sont le stress principales . Par conséquent, pour l'analyse de la fatigue, nous avons aussi trois options pour le facteur de sécurité correspondant à chacune des théories généralement acceptées de la résistance des matériaux.