 |
AutoFEM Analysis Analyse statique | ||||||
Analyse statique
L'objectif principal de l'analyse statique des structures est l'évaluation d'un état de contrainte d'une structure soumise à la constante dans le temps (statique) forces. Cette évaluation de l'état de stress est généralement effectuée dans le but de sonder les caractéristiques de conception adoptées contre le critère de résistance. Le critère de résistance est généralement formulée comme suit:
La contrainte σ se développant dans une structure sous des forces externes appliquées doit être inférieure à la contrainte sûre [σ ] pour le matériel de structure donné après l'application de la marge du facteur de sécurité Ksafe.
![]()
Le module d'analyse statique du système de modélisation d'éléments finis avec AutoFEM sert au calcul d'un état de contrainte statique de structures en trois dimensions dans un environnement AutoCAD. Le module d'analyse statique travaille directement avec les modèles AutoCAD tridimensionnels et ne nécessite pas de constructions supplémentaires pour la résolution d'un modèle en trois dimensions.
Les principaux résultats d'une solution statique sont les suivants:
| • | Le champ des déplacements de structure dans les points de calcul du maillage d'éléments finis; |
| • | champ de déformation relative; |
| • | champ des composants de contrainte; |
| • | énergie de déformation; |
| • | réponse noeud (forces de réaction); |
| • | le domaine de la distribution du facteur de sécurité de contrainte sur le volume de la structure. |
| • | estimation d'erreur de contrainte |
Ces données sont normalement assez pour prédire le comportement de la structure et de prendre des décisions pour l'optimisation de la forme géométrique d'un objet dans le but d'assurer les principaux critères de résistance des pièces.
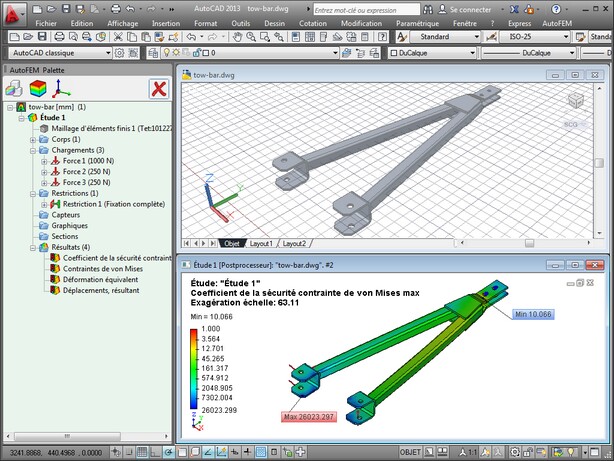
Les étapes en détail de l'analyse statique
L'analyse d'un modèle statique est réalisée en plusieurs étapes. Indiquées sont les éléments nécessaires pour procéder à une analyse.
Pour exécuter une analyse statique, procédez comme suit:
Pas 1. Création d'un modèle solide tridimensionnel d'un objet.
Avant de commencer à travailler avec AutoFEM, vous devez préparer un modèle solide en trois dimensions à évaluer. Un modèle peut être construit dans l'environnement AutoCAD ou importé d'autres systèmes. L'analyse statique peut être réalisée sur une ou plusieurs corps.
Pas 2. Créer l'«étude».
Vous pouvez utiliser une des façons suivantes pour créer l'étude:
Commande: |
_FEMASTUDY |
Menu principal: |
AutoFEM | Créer une étude... |
Icône: |
|
Vous devez également spécifier le type ("Analyse statique») de l'étude dans la fenêtre des propriétés de la commande.
S'il y a plusieurs corps dans la scène, vous devez sélectionner un ou plusieurs corps se touchants pour lesquels une nouvelle étude pourra être créée.
Pas 3. définir le matériel.
L'un des éléments requis pour toute solution est le matériel des objets de l'étude. La description détaillée du matériel définir des méthodes de calcul est fournie dans la section correspondante de la description préprocesseur.
Pas 4. Créer maillage.
Pour effectuer une modélisation d'éléments finis, vous devez construire un maillage d'éléments finis. Par défaut, la commande de la construction du maillage est lancée automatiquement lors de la création d'une étude. L'utilisateur peut également créer un maillage en utilisant la commande AutoFEM "AutoFEM | Create Mesh...". Lors de la création d'un maillage, l'utilisateur définit de différents paramètres discrétisant un modèle à l'état solide. Le maillage d'éléments finis peut influencer de manière significative la qualité de la solution obtenue dans le cas de la configuration spatiale de pièces complexes. Les paramètres de génération du maillage d'éléments finis sont examinés en détail dans la section respective de la description du préprocesseur AutoFEM.
Pas 5. Appliquer les conditions limites.
Dans l'analyse statique, conditions limites sont représentées par les méthodes et les charges externes appliquées aux restrictions. L'étape de création des conditions limites est très importante et nécessite une bonne compréhension de l'ingénieur de l'essence de l'étude étant résolu. Par conséquent, réfléchir aux aspects physiques de l'étude avant d'appliquer des conditions
limites est essentiel.
La définition de contraintes est une condition nécessaire à l'exécution d'une analyse statique correcte. La limitation combiné sur le mouvement du corps doit satisfaire la condition suivante:
Pour être adapté pour une analyse statique, un modèle doit avoir des restrictions qui empêchent la libre circulation dans l'espace comme un corps solide. A défaut de respecter cette condition entraîne des résultats erronés de l'analyse par éléments finis ou l'avortement de calculs.
Une commande est fournie dans AutoFEM pour définir les contraintes appelée «restriction». Le type "fixe" des contraintes définit un état totalement fixe (immobile) pour l'élément sélectionné du modèle. Le type "général" des contraintes permet de limiter le mouvement de l'élément de modèle le long des axes du système de coordonnées choisi.
La commande «Fixture» fournit également une autre fonctionnalité utile: Une ressource pour préciser des déplacements connus de la structure en elle. Pour cela, indiquez la valeur de déplacements d'un élément de modèle ainsi que quelques-uns des axes de coordonnées dans la fenêtre des propriétés de la commande "restriction". L'analyse statique sera réalisée prenant cette condition en compte. Notez qu'une solution statique est possible dans ce cas sans appliquer des charges supplémentaires (forces). De cette façon, nous pouvons évaluer la contrainte de développement dans une structure tendue lorsque les valeurs quantitatives de déplacements sont connus.
|
|
Exemple d'utilisation des déplacements connus |
|
Un certain nombre de commandes spécialisées est fourni dans AutoFEM pour définir les charges, voici les principaux types de charges ("Force", "Pression", "Force centrifuge", "Accélération", "Chargements de palier", "Moment de torsion"). Une description détaillée de tous les types de charges est fourni dans la description du préprocesseur.
Notez une capacité additionnelle d'un calcul statique AutoFEM. L'utilisateur peut définir l'analyse de l'état de stress d'une structure non seulement sous de forces diverses, mais aussi sous des charges thermiques - L'étude de «Thermoélasticité": Les matériaux de construction développent des déformation linéaire sous l'effet thermique - s'élargissent et se rétrécissent sous des changements de chaleurs. Les changements des dimensions d'un corps créent une tension et un état de stress. AutoFEM peut représenter cette évolution des températures. Pour définir des températures des champs de température transitoires, utilisez la commande:
Commande: |
_FEMATEMP |
Menu principal: |
AutoFEM | Chargements/Restraints | Temperature... |
Icône: |
|
En même temps, vous devez activer l'option "Considérer effets thermiques" sur le [Thermoélasticité] dans la boîte de dialogue des paramètres de l'étude statique afin de tenir compte des contraintes thermiques dans la solution statique. Vous devez aussi définir la température de souche "zéro", qui correspond à l'état de non-stress du modèle, et définir le champ de température de travail (les détails sont dans les "Paramètres du processeur statique linéaire" de la section).
Pas 6. Exécuter les calculs.
Une fois un maillage d'éléments finis est construit pour le modèle et les conditions limites sont appliquées (contraintes et charges), vous pouvez commencer le processus de création et résolution des équations algébriques linéaires de l'analyse statique. Utilisez la commande suivante pour commencer à résoudre l'étude active:
Commande: |
_FEMASOLVE |
Menu principal: |
AutoFEM | Résoudre... |
Icône: |
|
Le calcul de l'étude sélectionnée peut être démarrée à partir du menu contextuel en cliquant sur ![]() sur le nom de l'étude sélectionnée dans l'arbre des études. Par défaut, la boîte de dialogue «Paramètres de l'étude» de l'analyse statique s'ouvre automatiquement avant les calculations. Dans cette boîte de dialogue, l'utilisateur peut définir les options et paramètres de la solution souhaitée ainsi que spécifier les types de données de la solution affichables dans l'arbre des études. Description détaillée des paramètres étude but est également disponible dans les "Paramètres de la statique linéaire processeur" de la section. La plupart des paramètres sont choisis par le processeur automatiquement en fonction du nombre de dimensions dans l'étude en cours des conditions aux limites résolu et imposé.
sur le nom de l'étude sélectionnée dans l'arbre des études. Par défaut, la boîte de dialogue «Paramètres de l'étude» de l'analyse statique s'ouvre automatiquement avant les calculations. Dans cette boîte de dialogue, l'utilisateur peut définir les options et paramètres de la solution souhaitée ainsi que spécifier les types de données de la solution affichables dans l'arbre des études. Description détaillée des paramètres étude but est également disponible dans les "Paramètres de la statique linéaire processeur" de la section. La plupart des paramètres sont choisis par le processeur automatiquement en fonction du nombre de dimensions dans l'étude en cours des conditions aux limites résolu et imposé.
En cliquant sur le bouton [OK] dans la boîte de dialogue le processus de construction et de résolution des systèmes d'équations algébriques linéaires est lancé. Les étapes de la résolution d'équations et les informations de références supplémentaires sont affichés dans un volet d'information spéciale. Cliquer sur le bouton [Fermer] dans le volet d'informations termine les calculs. "Fermez la fenêtre après le calcul" forcera la fermeture automatique de la fenêtre de surveillance après avoir terminé la résolution d'équations.
«Garder le document après la fin du calcul» force l'enregistrement automatique des résultats des calculs et toutes les données modifiées dans le document actif.
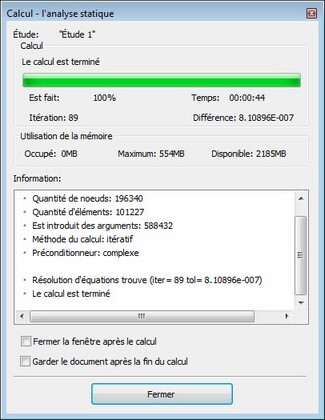
Les données de référence suivantes sont affichées dans la fenêtre d'information:
Noeuds - le nombre de nœuds dans le calcul fini maillage d'éléments.
Elements - le nombre de tétraèdres dans le maillage d'éléments finis.
Arguments - le nombre d'équations de la statique linéaire.
Type de calcul - l'algorithme utilisé pour résoudre les équations. Types d'algorithmes possibles et leur utilisation sont décrits dans la section "Paramètres du processeur statique linéaire "
Solution trouvée - indique que le système d'équations a été calculée avec succès. Il y a aussi des informations auxiliaires dans les parenthèses: iter - nombre d'itérations exécutées (si la méthode itérative a été utilisée), tol - erreur de calcul du résultat après calcul.
Pour le solveur d'itération, le numéro de l'itération en cours et l'erreur résiduelle de la solution sont présentées. Pour la méthode directe, le pourcentage du nombre total des équations résolues est signalée. L'utilisateur peut voir dans le mode temps réel, quel est le taux de résolution d'équations et de gérer ce processus. En outre, pour les deux méthodes de résolution, trois paramètres qui caractérisent le besoin en mémoire opérationnelle sont affichés: quelle quantité de mémoire est occupée par le solveur à l'instant, l'utilisation maximale et la quantité de mémoire opérationnelle disponible en total. Ces paramètres permettent à chaque utilisateur de déterminer si sa/son système informatique correspond à la solution d'un problème particulier.
Les étapes de calcul sont également affichés visuellement en tant qu'échelle dynamique. De plus, le temps écoulé depuis le début du calcul est affiché. Après la fin des calculs, l'utilisateur doit fermer la fenêtre auxiliaire (sauf si l'option "Fermer automatiquement" est activée).
Pas 7. Analyse des résultats de la solution statique.
Après avoir effectué les calculs, un nouveau dossier «Résultats» apparaît dans l'arbre des études. Par défaut, celui-ci affiche les résultats définis dans l'onglet "Résultats" de la boîte de dialogue "Paramètres de l'étude". Dans l'ensemble, l'utilisateur peut accéder à 38 solutions du résultat de l'analyse statique, triés en 6 groupes.
Le groupe «Déplacements» comprend les résultats suivants.
![]() - Composants du vecteur de déplacement pour un noeud du maillage d'éléments finis le long de l'axe OX du système de coordonnées global;
- Composants du vecteur de déplacement pour un noeud du maillage d'éléments finis le long de l'axe OX du système de coordonnées global;
![]() - Composants du vecteur de déplacement pour un noeud du maillage d'éléments finis le long de l'axe OY du système de coordonnées global;
- Composants du vecteur de déplacement pour un noeud du maillage d'éléments finis le long de l'axe OY du système de coordonnées global;
![]() - Composants du vecteur de déplacement pour un noeud du maillage d'éléments finis le long de l'axe OZ du système de coordonnées global;
- Composants du vecteur de déplacement pour un noeud du maillage d'éléments finis le long de l'axe OZ du système de coordonnées global;
Les déplacements, valeur absolue - la valeur absolue des déplacements des noeuds du modèle, défini pour chaque noeud d'après la formule:![]() , ou x, y, z - déplacement des composantes de vecteur pour le i-ième noeud de la maillage d'éléments finis.
, ou x, y, z - déplacement des composantes de vecteur pour le i-ième noeud de la maillage d'éléments finis.
Groupe «contraintes» comprend les résultats suivants:
![]() - contraintes équivalente relatives évaluée à partir de composantes du tenseur de contrainte selon la formule:
- contraintes équivalente relatives évaluée à partir de composantes du tenseur de contrainte selon la formule:![]() ;
;
![]() - la contrainte normale dans la direction de l'axe OX-du système de coordonnées global;
- la contrainte normale dans la direction de l'axe OX-du système de coordonnées global;
![]() - la contrainte normale dans la direction de l'axe OY-du système de coordonnées global;
- la contrainte normale dans la direction de l'axe OY-du système de coordonnées global;
![]() - la contrainte normale dans la direction de l'axe OZ-du système de coordonnées global;
- la contrainte normale dans la direction de l'axe OZ-du système de coordonnées global;
![]() - la contrainte de cisaillement agissant dans le sens de l'axe OY du système de coordonnées global parallèlement avec le vecteur normal à l'axe OX;
- la contrainte de cisaillement agissant dans le sens de l'axe OY du système de coordonnées global parallèlement avec le vecteur normal à l'axe OX;
![]() - la contrainte de cisaillement agissant dans le sens de l'axe OZ du système de coordonnées global parallèlement avec le vecteur normal à l'axe OX;
- la contrainte de cisaillement agissant dans le sens de l'axe OZ du système de coordonnées global parallèlement avec le vecteur normal à l'axe OX;
![]() - - la contrainte de cisaillement agissant dans le sens de l'axe OZ du système de coordonnées global parallèlement avec le vecteur normal à l'axe OY;
- - la contrainte de cisaillement agissant dans le sens de l'axe OZ du système de coordonnées global parallèlement avec le vecteur normal à l'axe OY;
![]() - stress principal
- stress principal ![]() .
.
L'intensité du stress est définie de la manière suivante: ![]()
Estimation de l'erreur de stress. Ce résultat montre l'estimation de l'erreur de stress du calcul en pourcentages. L'estimation est tracée en valeur de l'élément (constant dans un seul tétraèdre). De grande valeur de l'erreur signifie qu'il y a une grande différence dans le calcul de la contrainte avec ses éléments voisins. Le résultat le plus fiable de calcul est atteint lors de l'estimation de l'erreur de contrainte quand sa distribution est uniforme. Pour plus d'informations sur l'estimation: International Journal for Numerical Methods in Engineering, vol. 24, 337-357 (1987) “A Simple Error Estimator and Adaptive Procedure for Practical Engineering Analysis” de O.C. Zienkiewicz et J. Z. Zhu)..
Groupe "Coefficient de la sécurité selon les contraintes" comprend les résultats suivants:
Coefficient de sécurité par contraintes équivalentes représente le rapport entre recevable pour un produit donné les contraintes matérielles structurelles [σ ] aux contraintes équivalentes:
![]()
Coefficient de sécurité de cisaillement est évalué comme suit:
![]()
Coefficient de sécurité de la contrainte normale est évaluée comme suit:
![]()
Le stress sûre d'un matériel est défini dans les propriétés du matériel dans la bibliothèque AutoCAD standard ou dans le champ approprié de la bibliothèque des matériaux de l'étude. La limite d'élasticité est acceptée comme la contrainte sans danger pour les matières plastiques.
Groupe «déformation» comprend les résultats suivants:
![]() - tensions équivalentes relatives exprimées en termes de composants du tenseur des déformations par la formule:
- tensions équivalentes relatives exprimées en termes de composants du tenseur des déformations par la formule:
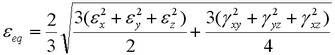 ;
;
![]() - Déformations de compressions dans la direction de l'axe OX du système de coordonnées global;
- Déformations de compressions dans la direction de l'axe OX du système de coordonnées global;
![]() - Déformations de compressions dans la direction de l'axe OY du système de coordonnées global;
- Déformations de compressions dans la direction de l'axe OY du système de coordonnées global;
![]() - Déformations de compressions dans la direction de l'axe OZ du système de coordonnées global;
- Déformations de compressions dans la direction de l'axe OZ du système de coordonnées global;
![]() - Déformations de cisaillement dans le plan OXY;
- Déformations de cisaillement dans le plan OXY;
![]() - Déformations de cisaillement dans le plan OXZ;
- Déformations de cisaillement dans le plan OXZ;
![]() - Déformations de cisaillement dans le plan OYZ;
- Déformations de cisaillement dans le plan OYZ;
![]() - déformations principales
- déformations principales ![]() .
.
Densité d'énergie de déformation. Ce résultat reflète la répartition du volume de l'énergie de déformation par rapport au modèle.
Groupe «Réactions». Le résultat reflète les forces qui s'accumulent dans les noeuds de soutien (fixe) du modèle d'éléments finis.
![]() - force de réaction dans la direction de l'axe OX du système de coordonnées global;
- force de réaction dans la direction de l'axe OX du système de coordonnées global;
![]() - force de réaction dans la direction de l'axe OY-du système de coordonnées global;
- force de réaction dans la direction de l'axe OY-du système de coordonnées global;
![]() - force de réaction dans la direction de l'axe OZ-du système de coordonnées global;
- force de réaction dans la direction de l'axe OZ-du système de coordonnées global;
La force de réaction (valeur absolue) - la grandeur de la valeur absolue des forces de réaction de noeuds du modèle défini par un noeud en tant que ![]() , ou
, ou ![]() - x-composante,
- x-composante, ![]() - y-composante,
- y-composante, ![]() – z-composante de la force de réaction pour le i-ième noeud du maillage d'éléments finis.
– z-composante de la force de réaction pour le i-ième noeud du maillage d'éléments finis.
Le groupe "Chargement total» affiche les charges appliquées à un modèle d'éléments finis que les réponses de noeud efficaces. Ce type de données représente des informations de référence.
Temperature. Ce résultat montre la distribution de champs de températures dans le volume du modèle.
Algorithme d'analyse statique
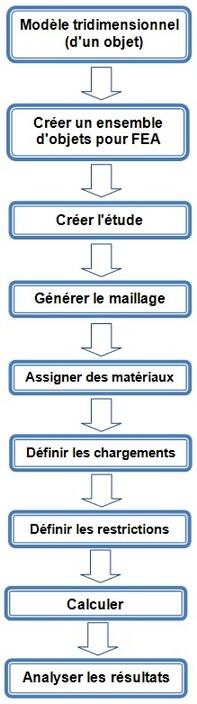
Algorithme pour l'évaluation statique de la résistance basée sur la modélisation
Un fois le calcul de l'étude est terminée avec succès, vous devez analyser les résultats obtenus afin de tirer des conclusions sur la résistance statique de la structure. Dans la plupart des cas, trois types de solutions suffisent - les déplacements, le stress et le facteur de sécurité. Une séquence type d'étapes pour valider les résultats de modélisation d'éléments finis est la suivante:
| 1. | L'analyse du déplacement. Dans l'arbre des études, utilisez dans le menu contextuel la commande "Ouvrir" ou "Ouvrir dans une nouvelle fenêtre" pour ouvrir la solution "Déplacement, résultants". Nous pouvons estimer visuellement le modèle et les plages de l'état de déformations d'une structure. Il est nécessaire d'analyser les déplacements afin de vérifier l'exactitude des charges appliquées et de la solution trouvée à la suite de la résolution des systèmes d'équations. Si les résultats de l'analyse des déplacements ont indiqué qu'une solution est trouvée à l'étude et le modèle de l'état de déformation de la structure correspondant à l'attendu vous pouvez passer à l'étape suivante.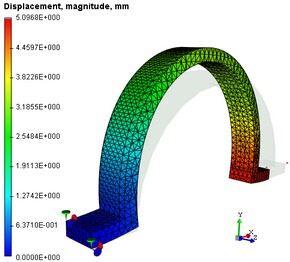  Le schéma de déplacements absolus et de contraintes équivalentes |
| 2. | Analyse des contraintes. Ouvrez le résultat "contraintes équivalente". Nous pouvons y évaluer visuellement l'assurance calculé et le schéma de la contrainte équivalente. Les gradients de stress sont illustrés par des transitions de couleurs. L'échelle de code couleur affiché dans la fenêtre des résultats de calculs aide a visionner la valeur approximative du résultat affiché. Si vous pointez la souris sur une zone d'intérêt sur le modèle une info-bulle s'affiche, montrant la valeur de la mesure évaluée, interpolée par les nœuds les plus proches autour de l'emplacement du pointeur. Le résultat "contrainte équivalente" permet à l'utilisateur de tirer les conclusions suivante à la suite: a) Déterminer, à quels endroits et dans quel élément de la structure la plus grande contrainte s'est développée; b) En comparant les maxima de la contrainte calculée avec la contrainte admissible pour le modèle de matériel, nous pouvons évaluer le degré de la résistance structurelle. |
| 3. | Estimation du coefficient de sécurité. Ouvrez le résultat "coefficient de sécurité équivalent du stress". Ce résultat permet d'estimer le rapport quantitatif de la contrainte de sécurité à la contrainte équivalente calculée est spécifié dans les propriétés du matériel. Par défaut, le résultat s'affiche sur l'échelle logarithmique afin de réduire la gamme de couleurs. Si le rapport de la contrainte calculée est sûr et approches devient 1 ou moins que cela, alors le critère de résistance ne tient plus et, par conséquent, la conception doit être modifiée. |
Réglages du processeur statique linéaire et non linéaire
Les propriétés de l'étude définies par l'utilisateur sont enregistrés avec le document et sont héritées lors de la copie d'une étude. Le but principal des propriétés de l'étude est de définir les options pour le processeur, les listes de résultats à afficher après avoir terminé les calculs dans les études d'arbres, ainsi que de garder les attributs descriptifs de l'étude, comme le nom ou un commentaire. La boîte de dialogue des paramètres de la solution d'analyse statique comporte cinq onglets:
[Général] sert à définir les propriétés descriptive de l'étude en cours.

Dans le champ "Nom", l'utilisateur peut modifier le nom attribué à l'étude par défaut lors de la création. Ce nom sera affiché dans l'arbre d'étude, dans la fenêtre des résultats et dans le rapport. Le champ "Type" sert à définir le type d'étude. Notez qu'AutoFEM permet de changer le type d'étude existante à un autre de la liste des types d'études disponibles. Par exemple, l'utilisateur peut créer une étude de type "Analyse statique", puis changer le type, par exemple, à «stabilité» ou "analyse de fréquence".
Le champ "Commentaire" permet à l'utilisateur d'entrer des informations de texte concernant l'étude. Cette information sera utilisée à l'avenir pour générer un rapport basé sur les résultats de la solution de l'étude.

L'onglet [Calcul] sert à définir les propriétés du processeur pour résoudre des équations linéaires statiques. Les éléments de contrôle dans la "méthode de calcul" groupe permet à l'utilisateur de définir les méthodes de systèmes d'équations algébriques de statique linéaire résoudre.
Automatique. Le solveur choisit la méthode de résolution d'équations basées sur le nombre d'équations. Si le nombre d'équations dépasse le seuil fixé dans les Paramètres du compte AutoFEM (la valeur par défaut est réglé à 100.000), le système d'équations est résolu par une méthode itérative, si le nombre d'équations est inférieure à la limite spécifiée, la méthode directe est choisie.
Méthode directe. Le système d'équations est résolu par la méthode de Gauss par décomposition LU de la matrice de rigidité. Ce procédé est efficace pour la résolution des systèmes d'équations construits sur la base des éléments finis linéaires. Dans certains cas, l'utilisation de la méthode directe peut être également justifiée pour l'analyse du système à l'aide d'éléments finis quadratiques. Il peut être utilisé à la place de la méthode itérative, si l'algorithme itératif ne converge pas vers une solution stable, ou si la vitesse de convergence est très lente (le nombre d'itérations est de plusieurs milliers). Cette situation peut être observée pour des situations «minces» (le modèle est plat ou allongé), ainsi que pour un grand nombre d'éléments finis qui se différentie considérablement des éléments équilatéraux (lorsque le rapport des longueurs des arêtes des éléments finis sont sur l'ordre de centaines ou de milliers). Des paramètres supplémentaires de la méthode directe sont disponibles sous "Options".
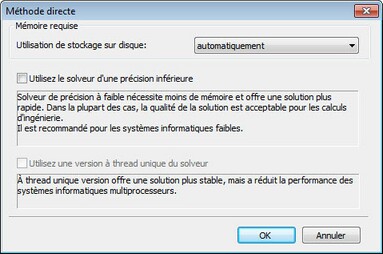
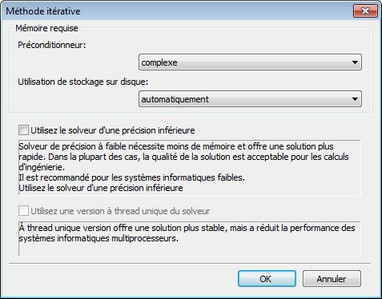
Itératif. Les systèmes d'équations sont résolues par la méthode itérative. Cette méthode est utilisée par défaut pour la résolution de systèmes d'équations construit sur la base d'éléments finis quadratiques. Les deux options suivantes peuvent être définies pour la méthode itérative: tolérance relative et le nombre maximum d'itérations. Des paramètres supplémentaires de la méthode itérative sont disponibles sous "Options".
Utilisation de la mémoire disque supplémentaire. L'utilisateur peut également gérer l'interaction avec externe mémoire (disque) du système informatique lors de la résolution des équations par la méthode directe ou itérative ([Options]). Il y a trois options pour l'utilisation de la mémoire du disque additionnel: automatique, interdite, obligatoire. L'utilisation de la mémoire de disque supplémentaire vous permet de sauvegarder la décomposition de la matrice de rigidité. L'utilisation de la mémoire disque supplémentaire pour la résolution des systèmes d'équations est nécessaire uniquement lorsque le besoin de mémoire pour garder matrices intermédiaires dépasse la mémoire RAM de l'ordinateur. Notez également que la durée du calcul des études avec un grand nombre de dimensions à l'aide de stockage externe pourrait être importante en raison d'un grand nombre d'opérations de lecture-écriture sur des données séquentielles.
Des volumes élevés de stockage sur disque peuvent être nécessaires pour garder les matrices intermédiaires (jusqu'à plusieurs gigaoctets). Assurez-vous qu'il y a suffisamment d'espace disque avant de résoudre les études de grandes dimensions à l'aide de stockage externe.
Si l'utilisateur a désactivé la possibilité d'utiliser l'espace disque tout en résolvant un système d'ordre élevé d'équations, le processus de calculs peut être avorter. Pour garder en mémoire la décomposition de la matrice près de 2 giga-octets sont recommandés (pour Windows 32-bits ).
La possibilité de lancer le solveur faible précision. Ce mode consomme près d'un tiers moins de mémoire opérationnelle et, en outre, les calculs s'effectuent plus rapidement. Dans la plupart des cas, la précision de la résolution des équations est suffisante pour les calculs d'ingénierie. Cette option peut être appliquée si l'utilisateur dispose d'un ordinateur suffisamment puissant. Par défaut, le solveur de précision normale est utilisé. En outre, il est possible d'exécuter le solveur de précision faible dans un mode de processeur unique.
Type de Préconditionneur (pour la méthode itérative). Quatre types de préconditionneurs sont disponibles.
Préconditionneur combiné est la méthode la plus rapide et par défaut. Il consomme quantité maximale de mémoire.
Décomposition incomplète, il faut une mémoire supplémentaire, dont le montant est égal à la mémoire, occupée par la matrice de rigidité.
Préconditionneur diagonal et d'identité, ils n'utilisent pratiquement pas de mémoire supplémentaire mais offrent un faible taux de convergence.
L'exactitude relative - la précision de la solution itérative atteinte. plus l'erreur est petite, plus de nombres d'étapes (itérations) seront nécessaire.
Le nombre maximum d'itérations - le nombre critique d'itérations, qui, après avoir été atteint, termine la résolution itérative du système d'équations, même si la précision de la solution requise n'a pas été atteinte.
Précision de résolution des restrictions de contact. Ce paramètre indique le pourcentage relatif des noeuds de contact qui sont exclus à chaque étape du processus itératif au cours du calcul des conditions limites. La valeur minimale est de 1%, maximale de 50%. Du point de vue de l'utilisateur, une valeur plus faible ralentit la solution du problème de contact, en même temps que la précision de la solution est augmentée.
Stabiliser le système non fixé. Habituellement, l'analyse de flambage d'un modèle non fixé qui est équilibré que par les forces est impossible. En raison d'erreurs d'arrondi le modèle se déplace dans l'espace ou tourne. Ces déplacements sont nettement plus importants que les déformations qui se produisent dans le modèle comme un résultat de l'action des forces statiques et ne nous permettent pas d'estimer l'état de déformation causé par les contraintes du système. Cela active la stabilisation du modèle dans l'espace non fixé. Le principe de la stabilisation est comme suit. Sur toutes les facettes du modèle des ressorts souples imaginaires sont appliquées. Il est supposé que la raideur des ressorts est négligeable par rapport à la raideur du matériel duquel le corps consiste. Par conséquent, ils n'ont pas d'incidence significative sur le résultat du calcul de stress. Mais ces sources ne permettent a éviter le déplacement incontrôlé du modèle dans l'espace. L'utilisateur peut choisir une valeur acceptable de raideur pour stabiliser le système dans chaque cas pratique.
Méthode des éléments finis. Par défaut, tous les calculs utilisent une approximation quadratique pour les déplacements, quel que soit le type de maillage d'éléments finis du modèle. Si l'utilisateur est seulement intéressé par les résultats qualitatifs, c'est qu'il est seulement intéressé par la distribution relative des champs de contraintes, en utilisant un maillage plutôt fin, il peut alors utiliser la solution d'éléments linéaires qui va beaucoup plus vite que la contrepartie quadratique. L'élément hybride est utilisé pour l'analyse de la résistance statique des modèles contenant à la fois des éléments de volume3D linéaire et en forme de plaques (dit modèles «hybrides» ).
L'analyse des éléments linéaire tétraèdre offre une précision insuffisante des résultats quantitatifs. Les résultats maximums de déplacement et le stress sont beaucoup plus petits via le calcul d'éléments finis tétraédriques linéaires, que ceux obtenus par des méthodes plus précises. Il est fortement recommandé d'utiliser des calculs d'éléments du second degré pour l'évaluation quantitative (le mode par défaut).
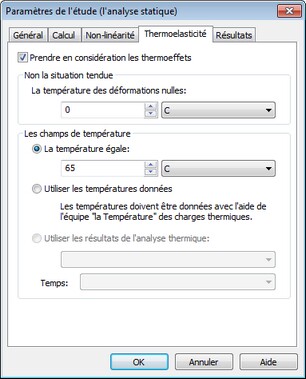
L'onglet [Thermoélasticité] permet de définir les méthodes de calcul des charges thermiques.
Prendre en considération les effets thermiques. Comprend le mode de calcul des charges s'accumulant dans une structure en raison des forces de dilatation linéaire dans les conditions de chaleur appliquées au corps.
La température des déformations nulles: - la température initiale du corps, à laquelle il n'y a pas de stress thermique et pas de contrainte provoquée par la différence de températures. L'utilisateur peut spécifier les valeurs de températures dans une des échelles existantes: K - Kelvins; C - Celsius; F- Fahrenheit.
Définir la méthode de spécification des charges thermiques dans le groupe "Les champs de température".
la température égale - la valeur d'un champ uniforme de la température est spécifié dans les unités choisies, ce qui affecte tous les corps étudiés.
Utiliser les températures données - les charges thermiques inclus dans l'analyse statique qui ont été définis par la commande "AutoFEM | Loads / Restraints | Temperature".
Utiliser les résultats de l'analyse thermique - Une solution disponible de l'étude d'analyse thermique est utilisée pour définir la charge thermique. Dans la liste déroulante, sélectionnez le nom de l'étude d'analyse thermique résolue et (si nécessaire) l'instant du temps qui fait l'objet des solutions. Veuillez noter que certaines conditions doivent être remplies pour l'utilisation des résultats d'analyse thermique comme les conditions initiales de température:
| 1. | Identifiez l'état du maillage d'éléments finis dans les analyses statiques et thermiques. La façon la plus simple de réaliser cela est l'utilisation de la commande "Copier" disponible dans le menu contextuel. La séquence des étapes peut être, par exemple, comme suit: a) Créer une étude de type «Analyse thermique", générez un maillage, définissez les conditions limites, et exécutez l'étude; b) Créez une copie de l'étude en utilisant la commande "Copier"; c) Dans l'onglet "Général" dans la boîte de dialogue des propriétés de l'étude, changez le type de l'étude à "analyse statique". |
| 2. | En conséquence, nous avons deux études de différents types, mais avec des maillages d'éléments finis identiques. |
| 3. | L'option «Calculer utilisant les éléments linéaire" dans l'onglet «Calcul» de la boîte de dialogue des paramètres de l'étude doit utiliser les mêmes paramètres dans les deux études. Par exemple, si l'analyse thermique est réalisé par des éléments linéaires, l'analyse statique basée sur les résultats d'analyse thermique peut également être exécuté uniquement avec des éléments linéaires. |
L'onglet [Résultats] permet de définir les types de résultats affichables dans l'arbre des études après la fin des calculs .

Sauvegarder les résultats du calcul dans le fichier - active le mode dans lequel tous les résultats d'analyse sont enregistrés dans le fichier avec le modèle. Cela permet d'analyser les résultats d'une étude calculée antérieurement et sauvegardée sans avoir besoin de répéter le calcul. Veuillez noter que l'enregistrement des résultats de calcul dans un document augmente la taille du fichier du document d'environ 4,5 à 5 Mo par cent mille degrés de liberté.
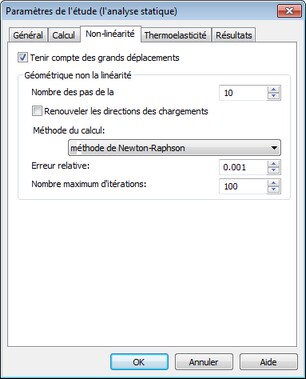
L'onglet [non linéaire] permet à l'utilisateur d'effectuer une analyse statique en tenant compte des grands déplacements.
Dans la pratique, il existe des situations dans lesquelles les déplacements de certains points de la structure atteigne des valeurs importantes sous l'action des charges externes. Ces problèmes sont particulièrement importants dans les aviation ou l'industrie spatiale, ou lors de la conception de radiotélescopes, tours de refroidissement et d'autres structures à parois minces. Dans ces cas, les effets non linéaires devraient être pris en compte, étant donné que les hypothèses sur lesquelles l'analyse linéaire est construite ne sont pas valides.
L'option "Tenir compte des grand déplacements" doit être activée dans le cas où au moins une des hypothèses suivantes de l'analyse linéaire est violée:
1. Déformations qui en résulte sont suffisamment petites, de sorte que les changements de rigidité causée par la charge peuvent être ignorés;
2. Dans le processus d'application de la charge, les conditions limites ne changent pas d'amplitude, de direction et de distribution.
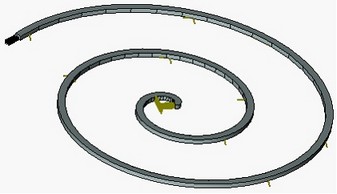
Par exemple, l'analyse linéaire de la partie en forme de spirale sous réserve de la charge appliquée au niveau du bord d'extrémité donne une erreur de l'ordre de 30% par rapport à l'analyse non linéaire. Cette différence dans les résultats se pose en raison de la supposition de petit déplacement adopté dans analyse linéaire.
|
|
analyse linéaire |
analyse non linéaire |
Les contrôles dans le groupe «non-linéarité géométrique» permettent à l'utilisateur de personnaliser le processus de solution des problèmes géométrique non linéaires.
Pour résoudre de tels problèmes, un solveur non linéaire organise le processus de chargement incrémentiel pas à pas de la structure et donne la solution du système d'équations linéarisé à chaque étape de l'incrémentation actuelle du vecteur de charge, formée d'une charge spécifique.
Nombre de prises en charges. Cette option permet à l'utilisateur de définir le nombre d'étapes au cours de desquelles la charge passe de zéro à une valeur spécifiée. Théoriquement, toutes les solutions se trouvent dans une étape pour la valeur totale de la charge. Cependant, il se pose la possibilité de non-unicité de la solution, et, en outre, la solution trouvée ne peut avoir aucune signification physique réelle. Dans de tels cas, il est raisonnable de spécifier la charge progressivement et obtenir une solution non linéaire pour chaque incrément. Du point de vue informatique, cela est souvent efficace parce que les effets non linéaires seront s'diminuent à chaque étape. Si les incréments de charge sont de suffisamment faible ampleur, chaque solution supplémentaire peut être trouvée dans une étape avec un haut degré de précision. Par défaut, le nombre de pas est fixé à 10.
Mettre à jour la direction de charge permet à l'utilisateur de tenir compte d'un changement du vecteur de charge tout en appliquant la charge en fonction de la géométrie déformée du modèle.
Méthode de solution. Par défaut, le procédé de Newton-Raphson de résolution de systèmes d'équations non linéaires sont utilisées. A chaque étape de l'application de la charge, le système des équations algébriques linéaires sont résolu tant que l'erreur relative entre deux solutions consécutives ne devient pas plus petit que la tolérance prescrite.
Si le nombre d'itérations atteint une valeur plus grande que celle spécifiée, les calculs sont terminés.
Annexe (références)
Propriétés des matériaux de construction
Une bonne affectation des propriétés des matériaux utilisés dans une structure est une condition importante pour l'exactitude de l'analyse des éléments finis. Les principales propriétés des matériaux de construction utilisés pour l'analyse de la force dans AutoFEM sont:
Module élastique E d'un matériel, [N/m2] - est le rapport de la contrainte par rapport à la souche parent ![]() développée dans un spécimen en forme de prisme soumis à une force axiale dans un essai de traction. Dans ce cas, un état de contrainte uniforme existe dans la partie médiane de l'échantillon dans la direction longitudinal. La valeur du module d'élasticité E sur le graphique de contrainte
développée dans un spécimen en forme de prisme soumis à une force axiale dans un essai de traction. Dans ce cas, un état de contrainte uniforme existe dans la partie médiane de l'échantillon dans la direction longitudinal. La valeur du module d'élasticité E sur le graphique de contrainte ![]() est numériquement égale à la tangente de l'angle d'inclinaison du segment linéaire:
est numériquement égale à la tangente de l'angle d'inclinaison du segment linéaire: ![]() sur le graphique de contrainte lors de l'essai d'un échantillon. Le sens physique du module d'élasticité E est décrite comme étant la contrainte nécessaire pour doubler la longueur de l'éprouvette. Toutefois, la valeur de l'allongement élastique atteint rarement 1% pour la plupart des corps solides.
sur le graphique de contrainte lors de l'essai d'un échantillon. Le sens physique du module d'élasticité E est décrite comme étant la contrainte nécessaire pour doubler la longueur de l'éprouvette. Toutefois, la valeur de l'allongement élastique atteint rarement 1% pour la plupart des corps solides.
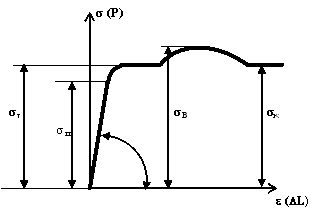
Le graphe de contraintes du spécimen testé a plusieurs points particuliers correspondant à des changements dans les propriétés physiques de la matière et est utilisée pour évaluer le degré de fiabilité du matériau sous charge.
Limite d'élasticité σп - la contrainte qui est la limite supérieure de l'effet de la déformation purement élastique.
Le Schéma de stress (dilatation) pour les matières plastiques (par exemple, l'acier à faible teneur en carbone)
Limite d'élasticité σТ. Un allongement d'avantage du spécimen (par exemple, pour les aciers à bas carbone) se produit pratiquement sans augmentation de la charge. Ce phénomène est appelé «écoulement plastique», et la partie horizontale du diagramme à la droite du point d'inflexion est appelée la gamme d'écoulement plastique. Dans de nombreux matériaux de construction la gamme d'écoulement plastique n'est pas bien visible, comme dans les aciers bas carbone. La notion de la limite d'élasticité conditionnelle σ s est introduit pour ces matériaux; c'est la contrainte correspondant à la valeur résiduelle souche (plastique) égale à s %. Habituellement, s = 0,2%. La limite de rendement pour les matières plastiques est choisi comme critère de résistance - la contrainte sûr maximale [sy]. Atteindre contraintes correspondant à la limite d'élasticité provoque des déformations plastiques irréversibles dans la structure, brisant ainsi sa viabilité et est donc un comportement inadmissible du point de vue de la sécurité.
SR - la résistance ultime (résistance rhéologique) est le stress, qui produit la rupture de la matière en cas de dépassement. Lors de l'augmentation de la charge, il existe un moment, après quoi, plus de pression s'accumule dans l'échantillon, sans augmenter, voire même sous une réduction de la charge, jusqu'à la rupture.
Le coefficient de Poisson µ caractérise la déformation transversale se développant dans un spécimen qui s'étire. Dans la zone élastique, la contrainte dans la direction transversale est ![]() ,
,
ou ε - la déformation dans la direction longitudinale,
µ - le coefficient de Poisson. Pour les matériaux isotrope, le coefficient de Poisson se situe dans la gamme ![]() .
.
Pour diverses nuances d'acier, E = 195-206 GPa, µ = 0.23-0.31; pour les alliages d'aluminium, E = 69-71 GPa, µ = 0.30-0.33.
Les propriétés élastiques de certains matériaux sont donnés dans le tableau (le dénominateur indique la propriété respective de compression).
Matériel |
propriété |
|
|
|
|
|
E, GPa |
σТ,MPa |
σE,,MPa |
δ, % |
ψ, % |
acier ST.3 |
200 |
240/240 |
450/- |
26 |
50 |
acier 15 |
200 |
210/210 |
350/- |
28 |
55 |
acier 45 |
200 |
340/340 |
610/- |
24 |
45 |
acier 30HGSA |
200 |
950/950 |
1200/- |
13 |
- |
Fonte S-Ch-15-32 |
150 |
- |
150/640 |
0,6 |
45 |
Fil de cuivre |
110 |
250/250 |
320/- |
15 |
- |
Duralumin D16 |
75 |
240/240 |
420/- |
18 |
- |
Delta bois (contreplaqué) |
20 |
- |
250/160 |
- |
- |
Textolite |
30 |
75/115 |
127/168 |
1,5 |
- |
Les propriétés de plasticité d'un matériel sont l'allongement relatif et la contraction par rapport à la rupture:
![]() ,
, ![]()
ou l0, F0 -la longueur de la partie de travail de l'échantillon et la surface de la section transversale avant la déformation;
lk - la longueur de la partie de travail de du spécimen après la rupture;
Fk - la zone finale de la section transversale au cou du spécimen après la rupture.
Les matières plastiques et matériaux cassants se distinguent par la quantité d'allongement au moment de la rupture. Les matériaux développent des valeurs suffisamment élevées ![]() au point de rupture sont considérés comme des matières plastiques; les matériaux avec allongement relatif
au point de rupture sont considérés comme des matières plastiques; les matériaux avec allongement relatif ![]() sont appelés friables. Pour les matières plastiques, lors de la compression de près l'état de rupture, la graphique
sont appelés friables. Pour les matières plastiques, lors de la compression de près l'état de rupture, la graphique ![]() est la même que dans le cas de la tension. Sous une contrainte de compression, les spécimens se raccourcissent, en attendant, ses dimensions transversales se développent. Pour certaines matières plastiques, il est impossible de trouver la contrainte analogue à la résistance rhéologique de traction due à l'aplatissement de l'objet.
est la même que dans le cas de la tension. Sous une contrainte de compression, les spécimens se raccourcissent, en attendant, ses dimensions transversales se développent. Pour certaines matières plastiques, il est impossible de trouver la contrainte analogue à la résistance rhéologique de traction due à l'aplatissement de l'objet.
Les matériaux fragiles présentent une bien meilleure capacité à résister à des sollicitations de compression, car pour ceux-ci, la souche de rupture de compression dépasse l'ultime multiforme de résistance à la traction. La rupture des matériaux fragiles en compression est due à la fissuration.
Volume contrainte-déformation à un point
L'état déformé à un point d'un corps déformable est décrit par le tenseur des déformations symétriques:
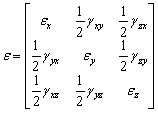 ,
,
ou ![]() - la tension de référence longitudinale,
- la tension de référence longitudinale,
![]() ,
, ![]() ,
, ![]() - la déformation angulaire. Vous pouvez toujours spécifier les trois directions orthogonales, de sorte que les angles abruptes soit tous zéros, tandis que allongements sont
- la déformation angulaire. Vous pouvez toujours spécifier les trois directions orthogonales, de sorte que les angles abruptes soit tous zéros, tandis que allongements sont ![]() . les tensions
. les tensions ![]() ,
, ![]() ,
, ![]() dans les directions, pour lequel angles abruptes sont absents, sont appelés tensions principaux en un point.
dans les directions, pour lequel angles abruptes sont absents, sont appelés tensions principaux en un point.
Ensemble, les neuf composantes de la contrainte ( trois pour chacune des faces perpendiculaires) forment une entité physique appelée tenseur des contraintes en un point. Le tenseur est représenté par une matrice symétrique:
 ,
,
ou ![]() - la contrainte de compression-traction,
- la contrainte de compression-traction,
![]() ,
, ![]() ,
,![]() , - la contrainte de cisaillement.
, - la contrainte de cisaillement.
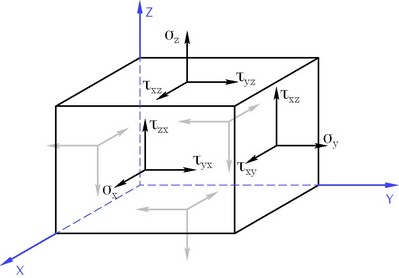
Les composantes du tenseur à l'état de stress dans un bloc infinitésimale
La règle suivante des signes est couramment utilisée pour les composants du tenseur de contraintes: un composant est positive, si elle pointe dans le sens positif de l'axe de coordonnées respectives d'une facette à la normale externe positive alignée avec l'une des coordonnées.
Le tenseur des contraintes et le tenseur des déformations possèdent la propriété de symétrie. ![]() ,
, ![]() ,
,![]() . Les conditions de symétrie du tenseur des contraintes sont aussi appelées contraintes de cisaillement jumelées: les contraintes de cisaillement agissantes sur deux faces mutuellement perpendiculaires dans les directions orthogonales à l'arête de l'intersection de ces faces sont égaux en amplitude. Grâce à ces propriétés, des neuf composantes du tenseur des contraintes, il y en a six indépendantes.
. Les conditions de symétrie du tenseur des contraintes sont aussi appelées contraintes de cisaillement jumelées: les contraintes de cisaillement agissantes sur deux faces mutuellement perpendiculaires dans les directions orthogonales à l'arête de l'intersection de ces faces sont égaux en amplitude. Grâce à ces propriétés, des neuf composantes du tenseur des contraintes, il y en a six indépendantes.
Tout comme dans le cas de la déformation, le concept des contraintes principales est introduit dans un état de stress, ![]() , correspondant à des contraintes principales, en relation avec les composantes du tenseur des contraintes par l'équation:
, correspondant à des contraintes principales, en relation avec les composantes du tenseur des contraintes par l'équation:
![]() , ou
, ou
![]() ,
, 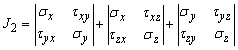 ,
, 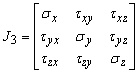
Une solution de l'équation cubique a trois racines réelles ![]() , qui sont communément classés comme suit:
, qui sont communément classés comme suit: ![]() . Les contraintes principales possèdent une propriété importante: les contraintes normales sur les faces direction axés principales sont les plus élevés comparé à ceux sur d'autres faces. Également introduit est le concept de contrainte moyenne par la formule
. Les contraintes principales possèdent une propriété importante: les contraintes normales sur les faces direction axés principales sont les plus élevés comparé à ceux sur d'autres faces. Également introduit est le concept de contrainte moyenne par la formule
![]()
L'évaluation de la force statique de la structure. Théories de la Force
L'état de stress de sécurité ultime est quand les propriétés des matériaux subissent un changement qualitatif - une transition d'un état mécanique à un autre. Pour les matières plastiques, l'état de contraintes sécuritaire est généralement considéré comme état de développement de la contrainte résiduelle notable, tandis que pour les friables c'est un état où un matériel commence à se fissurer. L'état final n'est pas admissible pour le matériel. Par conséquent, lorsque vous effectuez l'analyse des forces, poursuivez le État admissible. Cela correspond à la charge obtenue en divisant la charge de l'état de résistance ultime par le coefficient de sécurité. Si les facteurs de sécurité sont égaux dans les deux états ils sont appelés également sûr. Pour comparer les différents états tendues, la traction simple (compression) est accepté comme mesure universelle, avec la contrainte principale ![]() .
.
contrainte équivalente ![]() - le stress développé dans un spécimen étiré afin de rendre son état aussi incertain qu'un état sous contraintes spécifiées. Le critère de résistance est écrit que
- le stress développé dans un spécimen étiré afin de rendre son état aussi incertain qu'un état sous contraintes spécifiées. Le critère de résistance est écrit que ![]() .
.
Les théories de résistance sont des hypothèses au sujet des critères décrivant des conditions d'un matériel atteignant l'état de la résistance ultime.
Première théorie de force
Dans la première théorie de la force, la résistance à la rupture d'un matériel se réfère à la contrainte normale maximale. Selon cette théorie, l'état dangereux se produit lorsque l'une des principales contraintes atteint un seuil de sécurité. En conséquence, l'ampleur des contraintes maximales de capital est limitée de manière à ne pas dépasser la contrainte principale maximale ![]() . Le critère de résistance apparaît comme:
. Le critère de résistance apparaît comme: ![]() , ou
, ou ![]() , if
, if ![]() et
et ![]() , if
, if ![]() .
.
Deuxième théorie de force
La seconde théorie de la force utilise la contrainte maximale comme critère de résistance à la rupture. Selon cette théorie, l'état incertain d'un matériel se produit lorsque la déformation linéaire atteint un certain seuil de sécurité. Pour une matière plastique, le critère de résistance apparaît comme ![]() , ou
, ou ![]() . si, par exemple,
. si, par exemple, ![]() , alors
, alors ![]() .
.
Pour des matériaux friables, le critère de résistance apparaît comme:
![]() ,
, ![]()
La première théorie donne un bon accord avec les données expérimentales pour matériaux friables. La seconde est pratiquement abandonnée de nos jours.
Troisième théorie de force
Dans la troisième théorie de force, la résistance ultime se réfère à la contrainte maximale de cisaillement. Selon cette théorie, l'état incertain se produit lorsque la contrainte maximale atteint un seuil de sécurité.
Le critère de résistance apparaît en tant que ![]() , ou
, ou ![]() . En conséquence:
. En conséquence: ![]()
Quatrième théorie de la force (énergie)
La quatrième théorie de la force repose sur l'approche énergétique, basée sur l'hypothèse que la cause d'un état incertain est l'ampleur de la densité d'énergie potentielle de déformationuф, donc le critère de référence à la densité de l'énergie potentielle de déformation.
Nous allons dériver la formule de la densité d'énergie potentielle due à la distorsion de la formule de densité d'énergie potentielle totale due aux contraintes en utilisant le coefficient spécifique de Poisson de µ =0.5.
Ce qui donne:

Le critère de résistance apparaît comme![]() , ou
, ou 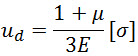 .
.
En conséquence:
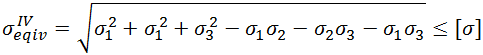
ou
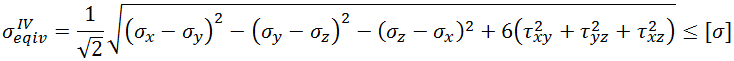
La troisième et quatrième théorie de résistance aboutissent à un accord satisfaisant des résultats des calculs théoriques avec les données de tests de laboratoires pour matières plastiques et sont largement utilisés dans l'analyse de la force. Ces théories ne sont pas applicables pour matériaux friables.