 |
 |
 |
 |
 |
 |
AutoFEM Analysis Integration Parameters |  |
|
|
|
|
|
|
AutoFEM Analysis Integration Parameters | |
Parameters of Time Integration
Difference scheme are used for the equations integration in both cases: Newmark or Wilson method.
Newmark method
The Newmark method is based on the following approximation of velocities and displacements:
,
,
where α, δ - parameters that determine the accuracy and stability of integration.
The parameters are set on the Parameters tab. Specifying of time integration parameters for the Newmark method is performed by pressing on the 
button near the method switcher. The parameters dialogue is opened in this case. By default, the parameters are configured to unconditionally convergence of the method.
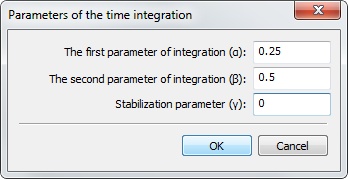
Newmark's integration parameters
For α=1/6, δ=1/2 accelerations vary linearly within the interval of integration; preferred for linear tasks;
For α=1/4, δ=1/2 accelerations remain constant within the interval of integration step. In this case the method unconditionally converge; used for nonlinear study. The condition of the method convergence on the assumption of proper choice of the time step: α >1/8.
Wilson method
The Wilson method is based on the fact that the vector of accelerations and loads vary linearly in the interval (t+θτ), where 
, based on the following approximation of the accelerations:
,
The expressions for velocities and displacements are received by integration of the equation:
,
Minimal value of θ=1,37, using which the method steadily converges, is θ=1,4.
Specifying of parameters for the Wilson method is performed by pressing on the 
button near the method switcher. By default, the integration parameters are configured to unconditionally convergence of the method.
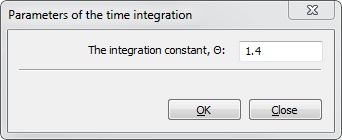
Wilson integration parameter
See also: Dynamic Analysis, Direct Time Integration, Mode Superposition, Dynamic Analysis Steps, Time Settings, Integration Parameters, Assigning Initial Conditions, Damping of System, Thermal Effects, Analysing Results, Example of Dynamic Analysis