 |
AutoFEM Analysis Analisi della Fatica | ||||||
Analisi della Fatica
Alcune parti di macchine, meccanismi e elementi architettonici nel processo di funzionamento sono sottoposti a carichi che variano con il tempo. Analisi delle sollecitazioni di problemi con tali carichi differisce dalla analisi per i carichi statici e di impatto. Il modulo di analisi di fatica del Analysis AutoFEM è utilizzata per studiare la forza sotto l'azione di carichi variabili. Affaticamento è un processo di graduale accumulo di danni nel materiale sotto l'influenza delle variabili di stress, portando alla formazione di crepe, sviluppo ed eventuale distruzione della struttura.
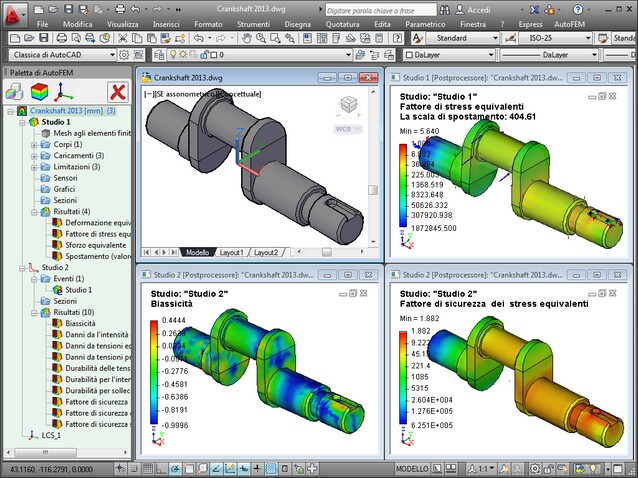
Dettagli dei passi dell'Analisi della Fatica
Prima di eseguire il calcolo della resistenza, si deve prima di esplorare l'effetto del carico statico sulla voce o struttura data (cioè eseguire un analisi statica). Ciò è necessario per stabilire se un guasto prodotto in un dato carico statico. Se il disegno viene distrutto in un determinato carico statico (il fattore di sicurezza minore di 1), quindi eseguire l'analisi della fatica non ha senso.
Un problema preliminare calcolo analisi statica è necessaria anche perché l'analisi delle sollecitazioni statiche calcolato (principale o equivalente) viene utilizzato per calcolare la resistenza a fatica come ampiezza di sollecitazioni cicliche.
Inoltre, per l'analisi della fatica è necessario che la curva S-N è stato determinato per il materiale da cui il prodotto è fabbricato. Creare il problema di analizzare affaticamento.
È possibile utilizzare uno dei seguenti modi per creare studio:
Command Line: |
_FEMASTUDY |
Main Menu: |
AutoFEM | Creare Studio... |
Icon: |
|
Allora avete bisogno di specificare il tipo di studio "analisi della fatica" nella finestra delle proprietà.

Per la creazione del ciclo di fatica si deve:
| 1. | Richiamare la finestra delle proprietà del ciclo di fatica scegliendo il gruppo "Eventi" dal albero studio nella finestra "AutoFEM Palette" e di eseguire il comando "Aggiungi ..." dal menu contestuale (premendo |
| 2. | Aggiungere lo studio statico che deve essere già stato calcolato. |
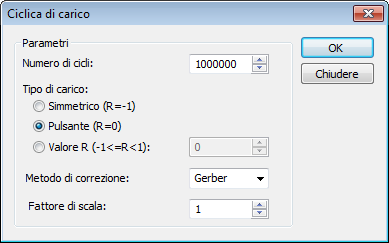
| 3. | Impostare i parametri del ciclo di fatica: numero di cicli, rapporto di sollecitazione, fattore di scala. |
| 4. |
Si può effettuare analisi di fatica per diversi eventi da studi statici differenti. Per esempio, se due o più forze sono ciclici ma hanno una legge diversa variabile. Va notato che l'elemento finito maglie della tesi studi statici devono essere identiche, e lo stesso corpo di ciascuno studio deve avere lo stesso materiale.
Inoltre è possibile impostare "Fattore di concentrazione dello stress" sulla scheda "fatica" della "Proprietà di studio (Analisi della Fatica)" finestra di dialogo, per impostazione predefinita è uguale a 1.
I risultati dell'analisi della fatica
Dopo aver eseguito il calcolo una nuova cartella chiamata "Risultati" viene creata nell'albero studi. Si può specificare l'elenco di risultati visualizzati sulla scheda "Risultati" delle "Proprietà di studio (Analisi della Fatica)" finestra di dialogo.

In tutti i dieci risultati sono disponibili per l'analisi della fatica. Essi possono essere suddivisi in quattro gruppi.
Gruppo "Danno" include i seguenti risultati:
| • | danni da tensioni principali (ipotesi 3); |
| • | danni da stress equivalenti (ipotesi 2); |
| • | danni da intensificazione degli sforzi (ipotesi 1); |
Questo risultato viene visualizzato in percentuale e indica il tasso danni della struttura sotto l'azione di sollecitazioni cicliche in un determinato numero e la natura dei cicli di carico.
Se il progetto presentato al n1 cicli di sollecitazione alternata S1, n2 cicli di sollecitazione alternata S2, n3 cicli di sollecitazione alternata S3, ..., nk cicli di sollecitazione alternata Sk, la valutazione di danno totale viene calcolato come: D = n1 / N1 + n2/N2 + n3/N3![]() +...+ nk/Nk , dove Ni è il numero di cicli necessari per causare distruzione Si.
+...+ nk/Nk , dove Ni è il numero di cicli necessari per causare distruzione Si.
Gruppo "Vita Totale" (questo tipo di risultato è disponibile solo per lo studio analisi della fatica singolo evento) comprende i seguenti risultati:
| • | vita totale per tensioni principali; |
| • | vita totale da stress equivalenti; |
| • | vita totale di intensificazione degli sforzi. |
Questo risultato indica il numero minimo di cicli Nmin, necessaria a provocare la rottura a fatica.
Gruppo "Fattori di Sicurezza" (questo tipo di risultato è disponibile solo per lo studio singolo evento analisi di fatica) include i risultati:
| • | fattore di sicurezza dalle sollecitazioni massime principali (ipotesi 3). |
| • | fattore di sicurezza per sollecitazioni equivalenti (ipotesi 2); |
| • | fattore di sicurezza da parte di intensificazione degli sforzi (ipotesi 1); |
Il fattore di sicurezza è il rapporto del limite di fatica σR, definita per una data curva di fatica per un dato numero di cicli di carico, corretto per l'ampiezza del ciclo σ*,che viene calcolato dai calcoli del problema di analisi delle sollecitazioni statiche σ:
![]()
Le sollecitazioni σ![]() sono calcolati sulla base delle condizioni pertinenti di plasticità:
sono calcolati sulla base delle condizioni pertinenti di plasticità:
| • | l'ipotesi di energia di distorsione: |
| • | l'ipotesi di sollecitazioni massime di taglio: |
| • | la più grande ipotesi di stress principale: |
Gruppo "Biassialità" (Questo tipo di risultato è disponibile solo per lo studio di analisi di fatica singolo evento) include il seguente risultato:
Biassialità è il rapporto tra la più piccola alternata tensione principale (diverso da 0) ad una tensione principale grande alternata.
![]() .
.
Questo risultato caratterizza la disuguaglianza delle ampiezze delle tensioni principali nel punto e descrive la distribuzione spaziale delle irregolarità delle sollecitazioni principali sul volume del corpo in ogni punto. Il valore della biassialità pari a 1 corrisponde al caso di stato uguale accento σ1=σ2=σ3 al punto.
Appendice (Riferimenti)
Il ciclo di stress. Le proprietà generali
Dopo un certo numero di carico ripetute (o cicli di sollecitazioni) la distruzione finale delle parti può verificarsi, d'altra parte, è possibile che la distruzione non avviene costantemente sotto carichi da stress. Il numero di cicli di sollecitazioni fino alla frattura dipende dalla grandezza, ampiezza della sollecitazione, e varia in un ampio intervallo. Per distruggere sotto elevate sollecitazioni 5-10 cicli sono sufficienti, d'altra parte, con sollecitazioni inferiori potrebbe resistere milioni o miliardi di cicli, e con sollecitazioni ulteriormente inferiori è in grado di operare a tempo indeterminato.
Ci sono massimo σmax e minimo σmin dei cicli di stress dai quali per capire il più grande e più piccolo del valore algebrico del ciclo di stress. Come una media di stress σm e ampiezza σa dei cicli di stress prende: σm= ( σmax + σmin ) / 2 , σa= ( σmax - σmin ) / 2. Scala di stress è chiamata differenza tra il ciclo massimo e minimo sforzo, i.e. 2σa= ( σmax - σmin ).
Il ciclo in cui il massimo e minimo sforzo in valore assoluto sono differenti è chiamato asimmetrico.
Un caso particolare del ciclo asimmetrico è ciclo pulsante nel quale il minimo del ciclo stress è zero: σmin = 0.
Un ciclo si dice simmetrico in cui le sollecitazioni massime e minime sono uguali in modulo ma di segno opposto.
Per caratterizzare il grado di asimmetria di stress viene utilizzato il rapporto asimmetrica stress, che è il rapporto tra minimo ciclo massimo sforzo: R=σmin/σmax .
Tipo di stress ciclico: |
asimmetrico |
pulsante |
simmetrico |
Rapporto di stress R=σmin/σmax : |
R1 |
0 |
-1 |
Minimo di stress σmin : |
R1*σmax |
0 |
- σmax |
Massimo stress σmax : |
σmax |
σmax |
σmax |
Media stress σm : |
(1 + R1 )*σmax/2 |
σmax/2 |
0 |
Ampiezza dello stress σa : |
(1 - R1 )*σmax/2 |
σmax/2 |
σmax |
Scala di Stress 2σa : |
(1 - R1 )*σmax |
σmax/2 |
2*σmax |
|
|
|
||
Ciclo asimmetrico ( R= - 0.2) |
Ciclo simmetrico ( R= -1 ) |
Ciclo pulsante ( R= 0 ) |
I metodi di correzione dello stress
Si supponga σ* è il corretto stress alternato, σY è il rendimento dello stress, σT è l forza tensile, allora:
| 1. | Metodo Soderberg σ* = σa / ( 1 - σm / σY ) |
| 2. | Metodo Goodman è utilizzato per materiali fragili: σ* = σa / ( 1 - σm / σT ) |
| 3. | Metodo Gerber è utilizzato per materiali plastici: σ* = σa / ( 1 - ( σm / σT )2 ) |
Valutazione delle caratteristiche di resistenza alla fatica sotto stato di sollecitazione complesso
Condizioni di resistenza con sollecitazioni alternate in termini generali simili alle condizioni di resistenza di analisi statica, ma come limite massimo ammissibile di stress utilizzato affaticamento σR . Di conseguenza, l'ipotesi criterio di forza prove di fatica per evitare deformazione plastica nei calcoli fatica prendono forma σ* ≤ σR ![]() . Ricordiamo le espressioni generali della verifica di ipotesi tradizionale di forza per la condizione di plasticità, utilizzati per valutare la resistenza delle strutture:
. Ricordiamo le espressioni generali della verifica di ipotesi tradizionale di forza per la condizione di plasticità, utilizzati per valutare la resistenza delle strutture:
| 1. | Tresca - Saint-Venant ipotesi (ipotizza la massima sollecitazione di taglio) σY < ( σ1 - σ3 ), | σ1 | ≥ | σ2 | ≥ | σ3 | |
| 2. | Huber - Mises ipotesi (ipotizza l'energia distorsione) |
| 3. | Mohr ipotesi (ipotizza la più grande sollecitazione principale) σY < σ1 , | σ1 | ≥ | σ2 | ≥ | σ3 | |
dove ![]() σY è il carico di snervamento, σ1 , σ2 , σ3 sono le principali tensioni. Pertanto, quando si analizza la fatica, abbiamo anche tre opzioni per il fattore di sicurezza corrispondente a ciascuno di teoria generalmente accettata di forza materiale.
σY è il carico di snervamento, σ1 , σ2 , σ3 sono le principali tensioni. Pertanto, quando si analizza la fatica, abbiamo anche tre opzioni per il fattore di sicurezza corrispondente a ciascuno di teoria generalmente accettata di forza materiale.