 |
AutoFEM Analysis Analisi Statica | ||||||
Analisi Statica
L'obiettivo principale dell'analisi di resistenza statica delle strutture è la valutazione di uno stato di stress di una struttura sottoposta costantemente nel tempo a forze (statiche). Questa valutazione dello stato di sollecitazione è di solito eseguita con lo scopo di sondare le caratteristiche progettuali adottate contro il criterio di resistenza. Il criterio di resistenza è generalmente formulato come segue:
Lo sviluppo dello stress σ in una struttura sotto forze esterne applicate deve essere inferiore alla pressione di sicurezza [σ ] per il dato materiale strutturale dopo l'applicazione del margine ceppo di fattore di sicurezza Ksafe.
![]()
Il modulo di analisi statica del sistema di modellazione AutoFEM elementi finiti serve per calcolare uno stato di stress statico di strutture tridimensionali in ambiente AutoCAD. Il modulo di analisi statica lavora direttamente con modelli AutoCAD tridimensionali e non richiede costruzioni aggiuntive per risolvere un particolare modello tridimensionale.
I principali risultati di una soluzione statica sono:
| • | il campo degli spostamenti della struttura nei punti di calcolo della maglia degli elementi finiti; |
| • | relativo campo di deformazione; |
| • | componenti di tensione di campo; |
| • | energia di stiramento; |
| • | risposta del nodo (forze di reazione); |
| • | il campo della distribuzione del fattore di sicurezza di trazione sul volume della struttura; |
| • | stima dell'errore di stress. |
Questo dato è normalmente sufficiente per prevedere il comportamento struttura e prendere decisioni per ottimizzare forma geometrica di una parte con l'obiettivo di assicurare principali criteri di resistenza di parti.
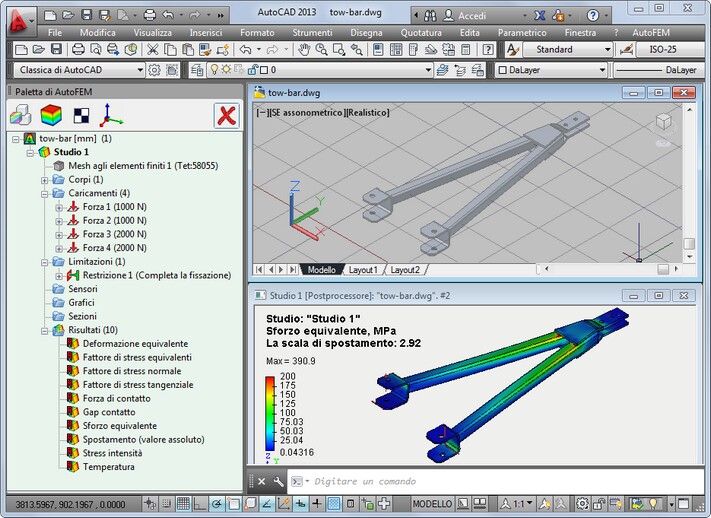
Dettagli dei passaggi dell'Analisi Statica
L'analisi statica di un modello viene eseguita in diverse fasi. Qui sono elencati i passaggi necessari per condurre un'analisi.
Per eseguire un'analisi statica, effettuare le seguenti operazioni:
Passo 1. Creazione del modello solido tridimensionale.
Prima di iniziare a lavorare nel sistema di AutoFEM, si dovrebbe preparare un modello solido tridimensionale da valutare. Un modello solido può essere costruito in ambiente AutoCAD o importato da altri sistemi. L'analisi statica può essere eseguita su una o più corpi.
Passo 2. Creare uno "Studio".
Si può usare uno dei seguenti modi per creare studio:
Command Line: |
_FEMASTUDY |
Main Menu: |
AutoFEM | Creare studio... |
Icon: |
|
Inoltre è necessario specificare il tipo di "Analisi statica" dello studio nella finestra delle proprietà del comando.
Se ci sono più "corpi" nella scena, si rende necessario selezionare uno o più corpi a contatto, per il quale verrà creato un nuovo studio.
Passo 3. Definire il materiale.
Uno degli elementi necessari di qualsiasi soluzione è il materiale dello studio. Descrizione dettagliata dei metodi di definizione dei materiali per i calcoli è previsto nella rispettiva sezione descrivente il processo di pre-elaborazione.
Passo 4. Creare la maglia.
Per eseguire la modellazione ad elementi finiti, è necessario costruire una maglia ad elementi finiti. Per impostazione predefinita, il comando di costruzione della maglia si avvia automaticamente durante la creazione di uno studio. L'utente può anche creare una mesh usando il comando AutoFEM "AutoFEM | Crea mesh ...". Quando si crea una maglia, l'utente definisce vari parametri di discretizzazione nel modello a stato solido. La maglia ad elementi finiti può influenzare significativamente la qualità della soluzione ottenuta nei casi di parti di complessa configurazione spaziale. I parametri generati dalla maglia ad elementi finiti sono esaminati in dettaglio nella relativa sezione che descrive l'AutoFEM pre-elaborazione.
Passo 5. Applicare le condizioni al contorno.
In analisi statica, le condizioni al contorno sono rappresentate da metodi restrittivi e carichi esterni applicati al sistema. La fase di costruzione di condizioni al contorno è molto importante e richiede una buona comprensione dal tecnico dell'essenza dello studio in osservazione. Pertanto è necessario riflettere su gli aspetti fisici dello studio prima di applicare condizioni al contorno.
Definire le limitazioni è una condizione necessaria per l'esecuzione di un'analisi statica corretta. La limitazione combinata al movimento del corpo deve soddisfare la seguente condizione:
un'analisi statica per essere razionalmente adeguata deve essere performata su un modello al quale sono posti degli ostacoli impedendo così la libera circolazione nello spazio del modello. Non riuscendo a soddisfare questa condizione si otterranno risultati errati di analisi agli elementi finiti o l'aborto di calcoli.
Un comando viene fornito in AutoFEM per la definizione di sistemi di ritenuta: "Fissaggio". Il tipo di "Fissaggio" dei vincoli definisce uno stato completamente immobile (fisso) per l'elemento del modello selezionato. Il "Generale" tipo di restrizioni consente di limitare i movimenti dell'elemento del modello lungo gli assi del sistema di coordinate prescelto.
Il comando "Fissaggio" fornisce anche un altro utile funzionalità. C'è una risorsa per specifici spostamenti noti per la struttura in esso. Per questo, si può specificare il valore di spostamento fisso di un elemento del modello lungo alcuni degli assi delle coordinate nella finestra "Fissaggio" del comando proprietà. L'analisi statica sarà eseguita con queste condizioni impostate. Si noti che una soluzione statica è possibile in questo caso senza applicare ulteriori carichi (forza). In questo modo, si può valutare lo stress di sviluppo in una struttura tesa quando sono noti i valori quantitativi della tensione (spostamenti).
.
|
|
Esempio dell'uso di spostamenti conosciuti |
|
Un certo numero di comandi specializzati è previsto in AutoFEM per definire i carichi tra i principali tipi di carichi ("Forza", "Pressione", "Forza Centrifuga", "Accelerazione", "Carico da cuscinetto", "Torsione"). Descrizione dettagliata di tutti i tipi di carichi è previsto nella sezione che descrive la pre-elaborazione.
Nota più di una capacità funzionale di una soluzione statica in AutoFEM, l'utente può definire l'analisi dello stato di stress di una struttura non solo sotto varie forze, ma anche in presenza di carichi termici - Lo studio delle "termoelasticità". Come è noto, i materiali strutturali sviluppano una tensione lineare sotto l'impatto termico - espandendosi per effetto del riscaldamento e contraendosi per effetto del raffreddamento. I cambiamenti nelle dimensioni del corpo causano tensioni ed uno stato di affaticamento. L'AutoFEM permette lo studio dei campi di transizione di temperatura considerando le variazioni di temperatura quando è usato il comando:
Command Line: |
_FEMATEMP |
Main Menu: |
AutoFEM | Carichi/Restrizioni | Temperature... |
Icon: |
|
Allo stesso tempo, è necessario attivare l'opzione "Consider Thermoeffects" sulla scheda [Thermoelasticity] dello studio statico parametri di dialogo al fine di tener conto dei carichi termici nella soluzione statica. Sarà inoltre necessario definire la temperatura di tensione "zero", che corrisponde allo stato di non-sollecitazione del modello, e per definire il campo di temperatura di lavoro (i dettagli sono nella sezione "Settings of Linear Statics Processor").
Passo 6. Eseguire i calcoli.
Una volta che una maglia ad elementi finiti è costruita per il modello e condizioni al contorno sono applicati (vincoli e carichi), è possibile avviare il processo o la creazione e la risoluzione di equazioni algebriche lineari dell'analisi statica. Utilizzare il seguente comando per cominciare a risolvere lo studio attivo:
Command Line: |
_FEMASOLVE |
Main Menu: |
AutoFEM | Solve... |
Icon: |
|
Il calcolo studi selezionato può essere avviato dal menu contestuale cliccando ![]() sul nome dello studio selezionato nell'albero studi.
sul nome dello studio selezionato nell'albero studi.
Per impostazione predefinita, la finestra di dialogo "Study parameters" della analisi statica si apre automaticamente prima di effettuare i calcoli. In questa finestra di dialogo, l'utente può definire le opzioni desiderate e le impostazioni del processo risolutivo, nonché specificare i tipi di dati della soluzione che vorranno essere visualizzabili nell'albero studi. La descrizione dettagliata delle impostazioni dell'obbiettivo dello studio è ulteriormente disponibile nella sezione "Settings of Linear Statics Processor". La maggior parte delle impostazioni sono selezionate dal processore automaticamente a seconda del numero di dimensioni nello studio che dovrà essere e delle condizioni al contorno.
Facendo clic sul pulsante [OK] nella finestra di parametri di studio si lancia il processo di costruzione e risoluzione dei sistemi di equazioni algebriche lineari. Le fasi di risoluzione delle equazioni e ulteriori informazioni di riferimento sono visualizzate in un apposito riquadro informazioni. Facendo clic sul pulsante [Chiudi] nel riquadro informazioni si terminano i calcoli. La bandiera "Close this dialog box on solving complection" costringerà la chiusura automatica della finestra di monitoraggio dei passi della soluzione al termine del processo risolutivo delle equazioni.
La bandiera «Save Document on solving completion» costringerà il salvataggio automatico dei risultati di calcolo e tutti i dati modificati nel documento attivo.
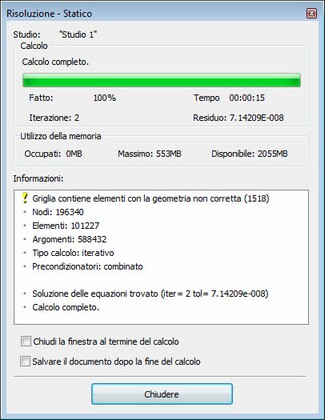
I seguenti dati sono presenti nella finestra delle informazioni al termine del calcolo:
Nodi - il numero di nodi nella maglia elementi finiti computazionale.
Elementi - il numero di tetraedri della maglia ad elementi finiti.
Argumenti - il numero di equazioni lineari statiche.
Tipo di calcolo -l'algoritmo utilizzato per risolvere le equazioni. Tipi di possibili algoritmi e il loro uso sono descritti nella sezione "Impostazioni della statica lineare processore".
Soluzione Trovata – dice che il sistema di equazioni è stato calcolato con successo. Ci sono anche informazioni ausiliarie nella parentesi: iter - il numero di iterazioni eseguite (se è stato utilizzato il metodo iterativo), tol - errore di calcolo del risultato dopo il calcolo.
Per il risolutore iterativo, il numero dell'iterazione corrente e l'errore residuo della soluzione sono presentati. Per il metodo diretto, viene mostrata la percentuale del numero totale delle equazioni risolte. L'utente può vedere in tempo reale, qual è il tasso di risoluzione delle equazioni, e gestire questo processo. Inoltre, per entrambi i metodi di risoluzione, tre parametri sono mostrati, che caratterizzano la necessità nella memoria operativa: la quantità di memoria occupata dal processo di risoluzione attualmente; massimo utilizzo; e la quantità di memoria operativa che è disponibile gratuitamente nel sistema al momento. Questi parametri consentono a ciascun utente di valutare se il suo sistema/calcolatore inserisce la soluzione di un problema particolare.
Le fasi di calcolo vengono visualizzate anche visivamente come una scala di aggiornamento dinamico. Inoltre, il tempo trascorso dall'inizio del calcolo è indicato. Dopo aver terminato i calcoli, l'utente deve chiudere la finestra ausiliaria (a meno che l'opzione di chiusura automatica è abilitata).
Passo 7. Analisi dei risultati della soluzione statica.
Dopo aver completato i calcoli, una nuova cartella "Risultati" viene visualizzata nell'albero studi. Per impostazione predefinita, questa visualizza i risultati definiti sulla scheda "Risultati" della finestra "parametri di studio". Nel complesso, l'utente può accedere a 38 soluzioni nel risultato dell'analisi statica, risolto in 6 gruppi.
Il gruppo "Spostamenti" include i seguenti risultati:
![]() - Componente di vettore spostamento per un nodo di elementi finiti lungo l'asse OX del sistema di coordinate globale;
- Componente di vettore spostamento per un nodo di elementi finiti lungo l'asse OX del sistema di coordinate globale;
![]() - Componente di vettore spostamento per un nodo di elementi finiti lungo l'asse OY del sistema di coordinate globale;
- Componente di vettore spostamento per un nodo di elementi finiti lungo l'asse OY del sistema di coordinate globale;
![]() - Componente di vettore spostamento per un nodo di elementi finiti lungo l'asse OZ del sistema di coordinate globale.
- Componente di vettore spostamento per un nodo di elementi finiti lungo l'asse OZ del sistema di coordinate globale.
Spostamento in valore assoluto – il valore assoluto degli spostamenti nodali del modello, definito per ogni nodo secondo la formula:
![]() , dove x, y, z - componenti vettoriali dello spostamento del nodo i-esimo della maglia ad elementi finiti.
, dove x, y, z - componenti vettoriali dello spostamento del nodo i-esimo della maglia ad elementi finiti.
Il gruppo «Tensioni» include i seguenti risultati:
![]() - sollecitazioni equivalenti date dalle componenti del tensore secondo la formula:
- sollecitazioni equivalenti date dalle componenti del tensore secondo la formula:
![]() ;
;
![]() - sollecitazione normale nella direzione dell'asse OX del sistema di coordinate globale;
- sollecitazione normale nella direzione dell'asse OX del sistema di coordinate globale;
![]() - sollecitazione normale nella direzione dell'asse OY del sistema di coordinate globale;
- sollecitazione normale nella direzione dell'asse OY del sistema di coordinate globale;
![]() - sollecitazione normale nella direzione dell'asse OZ del sistema di coordinate globale;
- sollecitazione normale nella direzione dell'asse OZ del sistema di coordinate globale;
![]() - sollecitazioni di taglio che agisce nella direzione dell'asse OY del sistema di coordinate globale su un piano con il vettore normale parallelo all'asse OX;
- sollecitazioni di taglio che agisce nella direzione dell'asse OY del sistema di coordinate globale su un piano con il vettore normale parallelo all'asse OX;
![]() - sollecitazioni di taglio che agisce nella direzione dell'asse OZ del sistema di coordinate globale su un piano con il vettore normale parallelo all'asse OX;
- sollecitazioni di taglio che agisce nella direzione dell'asse OZ del sistema di coordinate globale su un piano con il vettore normale parallelo all'asse OX;
![]() - sollecitazioni di taglio che agisce nella direzione dell'asse OZ del sistema di coordinate globale su un piano con il vettore normale parallelo all'asse OY;
- sollecitazioni di taglio che agisce nella direzione dell'asse OZ del sistema di coordinate globale su un piano con il vettore normale parallelo all'asse OY;
![]() - tensioni principali
- tensioni principali ![]() .
.
Intensità della tensione è definita nel modo seguente: ![]()
Errore nella stima della tensione. Questo risultato mostra la stima di errore di calcolo della tensione in percentuale. La stima viene tracciata come valore dell'elemento costante all'interno di un singolo tetraedro. Un grande valore di errore dell'elemento significa che è grande la differenza nel calcolo della tensione con i suoi elementi vicini. Il risultato più affidabile nel calcolo della tensione si raggiunge quando la stima dell'errore tende a distribuzione uniforme. Per ulteriori informazioni sulla stima dell'errore, consultare International Journal for Numerical Methods in Engineering, vol. 24, 337-357 (1987) “A Simple Error Estimator and Adaptive Procedure for Practical Engineering Analysis” by O.C. Zienkiewicz and J. Z. Zhu).
Group «Safety factor by stresses» include i seguenti risultati:
Safety factor by equivalent stresses representa il rapporto tra la tensione strutturale ammissibile per un dato materiale [σ ] con le tensioni equivalenti:
![]()
Safety factor by shear stresses è valutato come:
![]()
Safety factor by normal stresses è valutato come:
![]()
Lo stress di sicurezza di un materiale è definito nelle proprietà del materiale nella libreria standard di AutoCAD o nel campo appropriato della libreria dei materiali di studio. Il limite di resa è accettato come lo stress sicuro per materie plastiche.
Gruppo «Deformazione» comprende i seguenti risultati:
![]() - tensioni equivalenti relative espresse in termini dei componenti del tensore di deformazione dalla formula:
- tensioni equivalenti relative espresse in termini dei componenti del tensore di deformazione dalla formula:
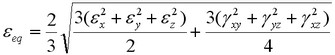 ;
;
![]() - relativa tensione normale nella direzione dell'asse OX del sistema di coordinate globale;
- relativa tensione normale nella direzione dell'asse OX del sistema di coordinate globale;
![]() - relativa tensione normale nella direzione dell'asse OY del sistema di coordinate globale;
- relativa tensione normale nella direzione dell'asse OY del sistema di coordinate globale;
![]() - relativa tensione normale nella direzione dell'asse OZ del sistema di coordinate globale;
- relativa tensione normale nella direzione dell'asse OZ del sistema di coordinate globale;
![]() - deformazione di taglio nel piano OXY;
- deformazione di taglio nel piano OXY;
![]() - deformazione di taglio nel piano OXZ;
- deformazione di taglio nel piano OXZ;
![]() -deformazione di taglio nel piano OYZ.
-deformazione di taglio nel piano OYZ.
![]() - deformazioni principali
- deformazioni principali ![]() .
.
Densità di energia di trazione. Il risultato riflette la distribuzione del volume di energia di deformazione rispetto al modello.
Groupo «Reazioni». Il risultato riflette le forze di costruire nelle supporto nodi (fissi) del modello elementi finiti.
![]() -forza di reazione in direzione dell'asse OX del sistema di coordinate globale;
-forza di reazione in direzione dell'asse OX del sistema di coordinate globale;
![]() - forza di reazione in direzione dell'asse OY del sistema di coordinate globale;
- forza di reazione in direzione dell'asse OY del sistema di coordinate globale;
![]() - forza di reazione in direzione dell'asse OZ del sistema di coordinate globale.
- forza di reazione in direzione dell'asse OZ del sistema di coordinate globale.
La forza di reazione (in valore assoluto) - la grandezza del valore assoluto delle forze di reazione nodali del modello definito per un nodo come ![]() , dove
, dove ![]() - componente-x,
- componente-x, ![]() - componente-y,
- componente-y, ![]() – componente-z della forza di reazione per il nodo i-esimo della maglia ad elementi finiti.
– componente-z della forza di reazione per il nodo i-esimo della maglia ad elementi finiti.
Il gruppo di “Carico Totale” visualizza i carichi applicati ad un modello ad elementi finiti come le risposte nodo efficaci. Questo tipo di dati rappresenta informazioni di riferimento.
Temperatura. Questo risultato mostra la distribuzione di campo di temperatura sul volume del modello.
Algoritmo dell'Analisi Statica

Algoritmo per valutare la Forza Statica sulla base di modelli
Una volta che il calcolo studio è stato completato con successo, si dovrebbe analizzare i risultati ottenuti al fine di trarre conclusioni sulla resistenza statica probabilistica della struttura. Nella maggior parte dei casi, tre tipi di soluzione sufficienti - spostamenti, sollecitazioni e il fattore di sicurezza ceppo. Una sequenza tipica di operazioni per convalidare i risultati di elementi finiti è il seguente:
| 1. | Analisi dello spostamento. Nell'albero di studi, utilizzare il comando del menu contestuale "Apri" o "Apri in una nuova finestra" per aprire la soluzione chiamata "Dimensione dello Spostamento". Possiamo stimare visivamente il modello e barre di stato sforzo-deformazione di una struttura. È necessario analizzare gli spostamenti al fine di verificare la correttezza dei carichi applicati e affermare la correttezza della soluzione trovata come risultato del sistema di equazioni risolte. Se i risultati delle analisi degli spostamenti indicano che si può trovare una soluzione allo studio e il modello dello stato di deformazione della struttura corrisponde a quanto previsto, allora si può procedere alla fase successiva. |
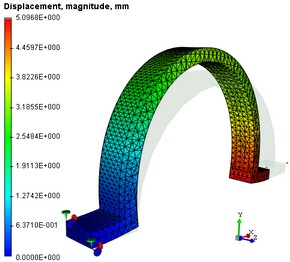
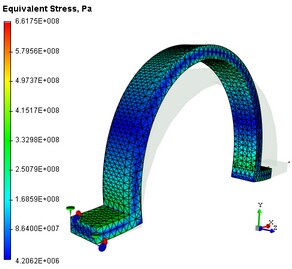
Il diagramma degli spostamenti assoluti e delle tensioni equivalenti
| 2. | Analisi della tensione. Aprendo il risultato "Tensione Equivalente". Si può valutare visivamente l'andamento della tensione equivalente calcolata. I gradienti della tensione sono illustrati da transizioni di colore. La scala di codice colore visualizzata nella finestra dei risultati di calcolo aiuta a leggere il valore approssimativo del risultato visualizzato. Se si punta il mouse sull'area di interesse del modello, poi un suggerimento si aprirà, visualizzando il valore della misura valutata, interpolati dai nodi più vicini intorno alla posizione del puntatore. Il risultato "Tensione Equivalente" consente all'utente di effettuare le seguenti conclusioni: a) determinare, in quale zona e in quali elementi della struttura si sviluppa il più grande sforzo; b) confrontando i massimi delle sollecitazioni calcolate con la tensione ammissibile per il materiale del modello, valutando il grado di resistenza. |
| 3. | Stima dei fattori di sicurezza. Aprire il risultato "Fattore di sicurezza per equivalente stress". Questo risultato permette di stimare il rapporto quantitativo della stres sicura alle sollecitazioni equivalenti calcolati specificati nelle proprietà del materiale. Per default, il risultato è mostrato sulla scala logaritmica per ridurre la gamma di sfumature di colore. Se il rapporto delle tensioni sicure e calcolati avvicina ad uno o diventa inferiore a quello, allora il criterio di resistenza non regge e, quindi, la progettazione deve essere modificata. |
Impostazioni del Processo di Analisi Statica Lineare e Non Lineare
Le proprietà di studio definiti dall'utente vengono salvate insieme al documento e sono ereditate dalla copia di uno studio. Lo scopo principale delle proprietà dello studio è di definire le opzioni richieste per il processore, nelle liste dei risultati che saranno visualizzate dopo aver completato calcoli nell'albero studi, oltre a mantenere gli attributi descrittivi dello studio, come il nome o commenti. La finestra di dialogo dei parametri della soluzione dell'analisi statica ha cinque schede.
La scheda [Generale] serve per definire le proprietà descrittive di questo studio.
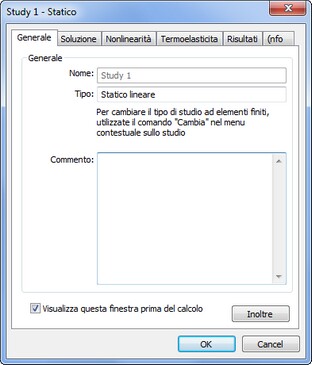
Nel campo "Nome", l'utente può modificare il nome dello studio assegnato di default dal sistema al momento della creazione. Questo nome sarà ulteriormente visualizzato nell'albero studi, nella finestra dei risultati e nella relazione. Il controllo "Tipo" serve per definire il tipo di studio. Si noti che AutoFEM permette di cambiare un tipo di studio esistente ad un altro dall'elenco dei tipi di studio disponibili per l'utente. Ad esempio, l'utente può creare uno studio di tipo "Analisi statica", e quindi modificare il tipo, ad esempio, in "Analisi della stabilità" o "Analisi della Frequenza".
La casella di modifica "Commento" permette all'utente di inserire le informazioni di testo arbitrario relative al corso di studio. Questa informazione verrà utilizzata in futuro per generare una relazione basata sui risultati della soluzione studio.
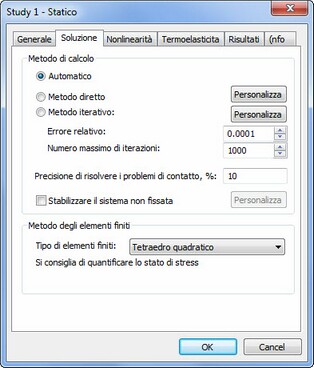
La scheda [Risolvere] serve per definire le proprietà dei processori per la risoluzione di equazioni lineari dell'analisi statica. Gli elementi di controllo nel gruppo "Metodo di calcolo" consentono all'utente di definire le modalità dei sistemi di equazioni algebriche della statica lineare da risolvere.
Automatico. Il risolutore sceglie il metodo per risolvere le equazioni in base al numero di equazioni. Se il numero di equazioni supera la soglia impostata nel AutoFEM Impostazioni (l'impostazione standard è di 100.000), il sistema di equazioni è risolto da un metodo iterativo, se il numero di equazioni è inferiore al limite specificato, il metodo diretto di soluzione è scelto.
Metodo Diretto. Il sistema di equazioni è risolto dal metodo di Gauss via decomposizione di LU della matrice di rigidità. Questo metodo è efficace per risolvere il sistema di equazioni costruite sulla base degli elementi finiti lineari. In alcuni casi, l'uso del metodo diretto può essere giustificato anche per analisi del sistema con l'aiuto di elementi finiti quadratici. Può essere usato al posto del metodo iterativo, se l'algoritmo iterativo non converge alla soluzione stabile, o se la velocità di convergenza è molto piccola (il numero di iterazioni è di parecchie migliaia). Questa situazione può essere osservata per problemi «sottili» (il modello è piatto o allungato), e anche per un gran numero di elementi finiti che sono notevolmente differenti da elementi equilateri (quando il rapporto tra le lunghezze dei bordi degli elementi finiti sono nell'ordine di centinaia o migliaia). Ulteriori impostazioni del metodo diretto sono disponibili col pulsante "Opzioni".
Iterativo. I sistemi di equazioni sono risolte con metodi iterativi. Questo metodo viene utilizzato nell'impostazione predefinita per risolvere sistemi di equazioni costruite sulla base di un elementi finiti di forma quadratica. Le seguenti due opzioni possono essere impostate per il metodo iterativo: tolleranza relativa e il massimo numero di iterazioni. Ulteriori impostazioni del metodo iterativo sono disponibili col pulsante "Opzioni"

Utilizzo di un ulteriore disco di memoria. Ulteriori utilizzo della memoria del disco. L'utente può anche gestire l'interazione con un disco di memoria esterno al sistema del computer quando risolve le equazioni con un metodo diretto o iterativo ([Opzioni]). Ci sono tre opzioni per l'utilizzo di un disco di memoria aggiunto: automatico, non disponibile, obbligatorio. L'uso di un disco di memoria aggiunto consente di salvare la decomposizione della matrice di rigidità. L'uso di un disco di memoria aggiuntiva per risolvere i sistemi di equazioni è necessario solo quando i requisiti di memoria per mantenere la matrice intermedia superano la RAM del computer. Si noti inoltre che il tempo di calcolo per studi con un gran numero di dimensioni che utilizzano la memorizzazione esterna potrebbe essere significativo a causa di un elevato numero di operazioni su dati sequenziali lettura-scrittura.
Alti volumi di archiviazione su disco possono essere necessari per mantenere le matrici intermedie (fino a diversi gigabyte). Assicurarsi che vi sia sufficiente spazio sul disco prima di risolvere gli studi di grandi dimensioni utilizzando un disco di archiviazione esterno.
Se l'utente ha disabilitato la possibilità di utilizzare lo spazio su disco durante la risoluzione di un sistema con un alto ordine di equazioni, un'interruzione anomala del processo può interrompere i calcoli per mantenere la decomposizione di una matrice nel caso di un consumo di memoria che si avvicinasse ai 2 Gigabyte (per Windows 32 bit).
La possibilità di lanciare il risolutore a bassa precisione. Questa modalità consuma quasi un terzo in meno di quantità di memoria operativa e, inoltre, i calcoli vanno più veloci. Nella maggior parte dei casi, si raggiunge una precisione della soluzione di equazioni che è sufficiente per i calcoli ingegneristici. Questa opzione può essere applicata se l'utente dispone di un computer sufficientemente alimentato. Di default, viene utilizzato il risolutore di precisione normale. Inoltre, è possibile lanciare il risolutore bassa precisione in una modalità singolo processore.
Tipo di Precondizionatore (per il modello iterativo). Quattro tipi di precondizionatori sono disponibili. Precondizionatore combinato è il metodo più veloce e di default. Si consuma una quantità massima di memoria. Decomposizione incompleta, richiede una memoria aggiuntiva, la cui quantità è uguale memoria occupata dalla matrice di rigidità. Diagonal e Identità Precondizionatore Diagonale e d'Identità, che praticamente non usa memoria aggiuntiva, ma fornisce un tasso più basso di convergenza
Accuratezza Relativa - l'accuratezza della soluzione iterativa raggiunta. Più è piccolo l'errore di calcolo specificato, e più grande sarà il numero di passaggi (iterazioni) richiesti.
Il Massimo Numero di Iterazioni - il numero di iterazioni critiche, dopo di che la soluzione iterativa del sistema di equazioni termina, anche se la precisione della soluzione richiesta non è stato raggiunto.
Accuratezza nella risoluzione delle restrizioni di contatto. Precisione di risolvere restrizioni di contatto. Questo parametro specifica la percentuale relativa dei nodi contatto che sono esclusi in ogni fase del processo iterativo durante il calcolo delle condizioni al contorno di contatto. Il valore minimo è 1%, il massimo il 50%. Dal punto di vista dell'utente, un valore minore rallenta la soluzione del problema di contatto, anche se la precisione della soluzione viene aumentata.
Stabilizzare il modello non fissato. Stabilizzare il modello non fissata. Di solito, il calcolo della resistenza statica del modello non fisso, che viene compensata soltanto da forze, è impossibile. A causa errori di arrotondamento il modello viene spostato nello spazio o ruota. Questi spostamenti sono significativamente più grandi delle deformazioni che si verificano nel modello a seguito dell'azione di forze statiche e non consentono di stimare lo stato di sforzo-deformazione del sistema. Questa "bandiera" accende la stabilizzazione del modello non fissato nello spazio. Il principio della stabilizzazione è il seguente. Su tutti gli aspetti del modello vengono applicate molle morbide immaginarie. Si presume che la rigidezza delle molle è trascurabile rispetto alla rigidità del materiale da cui è stato effettuato il corpo. Pertanto, esse non influenzano significativamente il risultato del calcolo statico. Ma questo molle non consentono il modello di muoversi nello spazio in maniera incontrollata. L'utente può scegliere un valore accettabile di rigidità per stabilizzare il sistema in ciascun caso pratico.
Metodo degli Elementi finiti. Metodo degli elementi finiti. Per impostazione predefinita, tutti i calcoli utilizzano un approssimazione quadratica per gli spostamenti, indipendentemente dal tipo di maglia ad elementi finiti con la quale è stato costruito il modello. Se l'utente è interessato solo a risultati qualitativi, cioè, egli è interessato solo nella distribuzione relativa dei campi di tensione, utilizzando una maglia piuttosto fine, allora uno può usare la soluzione dell'elemento lineare, che corre molto più veloce rispetto alla controparte quadratica. L'elemento ibrido viene utilizzato per l'analisi di resistenza statica dei modelli contenenti sia elementi di volume lastriformi e 3D lineari, cosiddetti modelli ibridi.
Nota! L'analisi con l'elemento tetraedrico lineare fornisce insufficiente accuratezza dei risultati quantitativi. Lo spostamento e la tensione massima dei risultati sono molto più piccoli attraverso il calcolo con gli elementi finiti tetraedrici lineari, piuttosto che quelli ottenuti con metodi più accurati. Si raccomanda vivamente di utilizzare i calcoli di elementi quadratici per la valutazione quantitativa (la modalità predefinita).
La scheda[Termoelasticità] consente di definire le modalità di calcolo dei carichi termici.

Considerare gli Effetti Termici. Include la modalità di calcolo dei carichi costruzione in una struttura dovuta alle forze di espansione lineare sotto la condizione di calore applicato al corpo.
Temperatura di zero deformazioni: - la temperatura iniziale del corpo, in cui non vi è alcuna tensione termica e non ci sono tensioni da differenza di temperatura. L'utente può specificare i valori di temperatura in una delle scale esistenti: K - Kelvins; C - Celsius; F- Farenheit. Definire il metodo per specificare i carichi termici nel gruppo "Campi di Temperatura".
Temperatura Uniforme - il valore di un campo di temperatura uniforme è specificato nella unità scelte, che colpisce tutti gli organi studiati.
Utilizzare una temperatura preimpostata - carichi termici sono inclusi nella analisi statica, che sono stati definiti dal comando "AutoFEM | Carichi / Vincoli | temperatura".
Utilizzare i risultati della funzione calore - soluzione disponibile dello studio di analisi termica viene utilizzata per definire il carico termico. Nell'elenco a discesa selezionare il nome dello studio analisi termica risolto e (se necessario) il tempo istantaneo, al quale la soluzione appartiene. Si prega di notare che alcune condizioni devono essere soddisfatte per l'utilizzo di risultati di analisi termica, come le condizioni di temperatura iniziali:
| 1. | Condizione di identità della maglia ad elementi finiti in analisi statiche e termiche. Il modo più semplice per raggiungere tale identità è l'uso del comando "Copia" disponibile nel menu contestuale. La sequenza di passi può essere, per esempio, come segue: a) Creare uno studio di tipo "Analisi termica", generare una mesh, definire condizioni al contorno, ed eseguire; b) Creare una copia di studio utilizzando il comando "Copia"; c) Nella scheda "Generale" nella finestra di proprietà di studio, ha cambiato il tipo di studio per "Analisi statica". Come risultato, abbiamo due studi di diverso tipo, ma con identiche maglie elementi finiti. |
| 2. | Il "Calcola usando l'elemento lineare" di proprietà della scheda "risolvere" della finestra di parametri di studio dovrebbero utilizzare le stesse impostazioni in entrambi gli studi. Ad esempio, se l'analisi termica è fatto da elementi lineari, allora l'analisi statica sulla base dei risultati di analisi termica può anche essere eseguito solo da elementi lineari. |
La scheda [Risultati] permette di definire i tipi di risultato visualizzabili nella struttura di studi dopo aver terminato i calcoli.
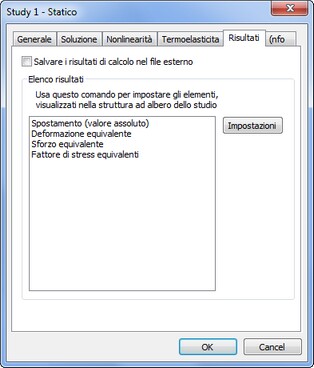
Salvare la soluzione dei risultati in un file - abilita la modalità, in cui tutti i risultati delle analisi vengono salvati nel file insieme al modello. Questo permette l'analisi dei risultati di uno studio calcolato e salvato in precedenza senza la necessità di un nuovo calcolo. Si prega di notare che il salvataggio dei risultati di calcolo in un documento aumenta la dimensione del file del documento di circa 4,5-5 Mbyte per centomila gradi di libertà.
La scheda [Info] mostra il tempo soluzione, versione del risolutore e vari parametri di soluzione.

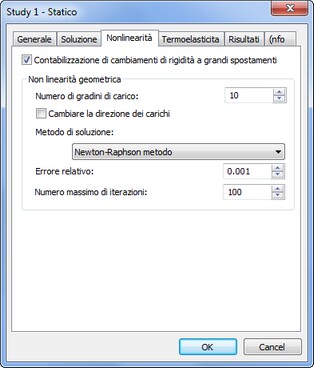
La scheda [Non lineare] permette all'utente di effettuare analisi statistiche prendendo in considerazione i grandi spostamenti.
In pratica, vi sono situazioni in cui gli spostamenti di taluni punti della struttura raggiungono valori significi sotto l'azione di carichi esterni. Questi problemi sono particolarmente importanti in aerei e nell'industria spaziale, durante la progettazione di radiotelescopi, torri di raffreddamento e altre strutture a pareti sottili. In questi casi gli effetti non lineari dovrebbero essere presi in considerazione, in quanto i presupposti su cui è costruita l'analisi lineare non sono valide.
L'opzione "Usa grande formulazione spostamento" dovrebbe essere attivato nel caso in cui almeno uno dei seguenti presupposti dell'analisi lineare è violato:
1. Deformazioni risultanti sono sufficientemente piccole, quindi le modifiche alla rigidità causata dal carico possono essere ignorate;
2. Nel processo di applicazione del carico, condizioni al contorno non cambiano l'ampiezza, la direzione e la distribuzione.
Ad esempio, l'analisi lineare della parte della spirale soggetta ad un carico applicato al bordo di estremità dà un errore di circa 30% rispetto all'analisi non lineare. Questa differenza nei risultati ottenuti è data da un piccolo spostamento assunto adottato dall'analisi lineare.
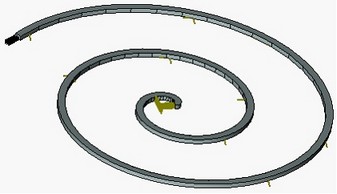
|
|
Analisi Lineare |
Analisi Non lineare |
I controlli nel gruppo «Geometrica non lineare» permettono all'utente di personalizzare il processo di soluzione dei problemi geometricamente non lineari.
Per risolvere tali problemi, un passo temporale del risolutore non lineare organizza il processo di caricamento incrementale della struttura e dà la soluzione del sistema di equazioni linearizzato ad ogni passo per l'incremento corrente del vettore di carico, formato per un determinato carico.
Numero di gradini di carico. Questa opzione permette di impostare il numero di passi in cui il carico cambierà da zero ad un valore specificato. Teoricamente, tutte le soluzioni si trovano a un passo per il valore complessivo di carico agente. Tuttavia, sorge la possibilità di non unicità della soluzione, e, inoltre, la soluzione trovata potrebbe non avere significato fisico. In tali casi, è ragionevole specificare il carico incrementale e ottenere una soluzione non lineare per ogni incremento. Dal punto di vista computazionale, spesso è efficace perché gli effetti non lineari saranno sempre più piccoli ad ogni passo. Se gli incrementi di carico saranno sufficientemente piccoli in grandezza, ogni soluzione incrementale può essere trovata all'interno di un passo con un elevato grado di accuratezza. Per impostazione predefinita, il numero di passi è impostato su 10.
Aggiornamento della direzione di carico. Consente di spiegare il cambiamento nel vettore carico, durante l'applicazione del carico, in funzione della geometria deformata del modello.
Metodo di Soluzione. Per impostazione predefinita, viene utilizzato il metodo di Newton-Raphson di risolvere il sistema di equazioni non lineari. Ad ogni passo di applicazione del carico, il sistema di equazioni lineari algebriche viene risolto finché l'errore relativo tra due soluzioni consecutivi non diventa inferiore alla tolleranza prescritta.
Se il numero di iterazioni raggiunge il valore maggiore di quello specificato, i calcoli sono terminati
Appendice (riferimenti)
Proprietà di Materiali Strumentali
Una corretta assegnazione delle proprietà dei materiali utilizzati nella struttura è un presupposto importante per la correttezza delle analisi agli elementi finiti. Le principali proprietà dei materiali strutturali utilizzati per l'analisi di forza in AutoFEM sono:
Il modulo elastioc di un materiale E, [N/m2] - è il rapporto tra la tensione rispetto alla tensione relativa ![]() sviluppare in un prisma a forma di provino sottoposto ad una forza assiale in una prova di trazione. In questo caso, uno stato di sollecitazione uniforme esiste nella metà parte del campione in direzione longitudinale. Il valore del modulo elastico E sul grafico ceppo
sviluppare in un prisma a forma di provino sottoposto ad una forza assiale in una prova di trazione. In questo caso, uno stato di sollecitazione uniforme esiste nella metà parte del campione in direzione longitudinale. Il valore del modulo elastico E sul grafico ceppo ![]() è numericamente uguale alla tangente dell'angolo di inclinazione del tratto lineare:
è numericamente uguale alla tangente dell'angolo di inclinazione del tratto lineare: ![]() sul grafico di stress nel test di un campione. Il senso fisico del modulo E è descritto come lo sforzo richiesto per raddoppiare la lunghezza del provino. Tuttavia, il valore di allungamento elastico raramente raggiunge anche 1% per la maggior parte dei corpi solidi.
sul grafico di stress nel test di un campione. Il senso fisico del modulo E è descritto come lo sforzo richiesto per raddoppiare la lunghezza del provino. Tuttavia, il valore di allungamento elastico raramente raggiunge anche 1% per la maggior parte dei corpi solidi.
Il grafico stress campione testato ha diversi punti particolari corrispondenti a cambiamenti delle proprietà fisiche del materiale e viene utilizzato per valutare il grado di affidabilità materiale sotto carico.
Limite di Elasticità σп - lo stress che è il limite superiore in effetto di deformazione elastica puramente.

Il diagramma delle tensioni (dilatazione) per materie plastiche (ad esempio, acciaio a basso tenore di carbonio)
Resa limite σТ. Ulteriore allungamento del campione (per esempio, per acciai a basso tenore di carbonio) avviene praticamente senza aumento del fenomeno è chiamato load.This "flusso plastico", e la parte orizzontale del diagramma immediatamente a destra dal punto di curvatura viene chiamato campo di flusso plastico. In molti materiali strutturali dell'intervallo di mandata plastica non è così ben visibile, come in acciai a basso tenore di carbonio. La nozione di limite di resa condizionale σ s viene introdotto per tali materiali; questa è la tensione corrispondente alla deformazione residua (plastica) pari a s%. Di solito, s = 0.2%. La Resa Limite per materie plastiche è selezionata come criterio di forza - il massimo tensione di sicurezza [sy]. Raggiungendo sollecitazioni corrispondenti al limite resa provoca deformazioni plastiche irreversibili nella struttura, rompendo così la sua vitalità ed è quindi un comportamento inammissibile dal punto di vista della sicurezza.
Il sr carico di rottura (resistenza reologico) è lo stress, al superamento che si verifica la rottura del materiale. A fronte di un aumento dei carichi, c'è un momento, dopo di che più sforzo si accumula nel campione senza un aumento, o anche in una riduzione, il carico, fino alla rottura.
Il coefficiente di Poisson µ caratterizza deformazione trasversale in via di sviluppo in un campione di stretching. Nella zona elastica, il ceppo in direzione trasversale è ![]() , dove ε - la deformazione in direzione longitudinale, µ— il coefficiente di Poisson.Per materiali isotropi, il coefficiente di Poisson trova nella fascia
, dove ε - la deformazione in direzione longitudinale, µ— il coefficiente di Poisson.Per materiali isotropi, il coefficiente di Poisson trova nella fascia ![]() .
.
Per vari tipi di acciaio, E = 195-206 GPa, µ = 0.23-0.31; per leghe di alluminio, E = 69-71 GPa, µ = 0.30-0.33.
Proprietà elastiche di alcuni materiali sono riportati nella tabella (il denominatore indica la rispettiva struttura di compressione).
Materiale |
Propiertà |
|
|
|
|
|
E, GPa |
σТ,MPa |
σE,,MPa |
δ, % |
ψ, % |
Acciaio ST.3 |
200 |
240/240 |
450/- |
26 |
50 |
Acciaio 15 |
200 |
210/210 |
350/- |
28 |
55 |
Acciaio 45 |
200 |
340/340 |
610/- |
24 |
45 |
Acciaio 30HGSA |
200 |
950/950 |
1200/- |
13 |
- |
Ghisa S-Ch-15-32 |
150 |
- |
150/640 |
0,6 |
45 |
Filo di Rame |
110 |
250/250 |
320/- |
15 |
- |
Duralluminio D16 |
75 |
240/240 |
420/- |
18 |
- |
legno Delta (compensato) |
20 |
- |
250/160 |
- |
- |
Textolite |
30 |
75/115 |
127/168 |
1,5 |
- |
Le proprietà di plasticità di un materiale sono il relativo allungamento e relativa contrazione a rottura:
![]() ,
, ![]()
dove l0, F0 -la lunghezza della parte lavorante del campione e l'area della sezione trasversale prima deformazione; lk - la lunghezza della parte lavorante del campione dopo la rottura; Fk - la zona finale della sezione a collo del campione dopo la rottura.
Gli stati di plastica e materiali fragili si distinguono per la quantità di relativa allungamento a rottura. Materiali sviluppo dei valori sufficientemente elevati ![]() al punto di rottura sono indicati come materie plastiche; quelli indicati come fragili sono i materiali con allungamento relativo di
al punto di rottura sono indicati come materie plastiche; quelli indicati come fragili sono i materiali con allungamento relativo di ![]() . Per i materiali plastici, compressi vicino alla condizione di rendimento,
. Per i materiali plastici, compressi vicino alla condizione di rendimento, ![]() disegno grafico è la stesso come nel caso della tensione. Sotto una deformazione di compressione, il campione si accorcia; Nel frattempo, le dimensioni della sezione trasversale crescono. Per alcuni materiali plastici, è impossibile trovare lo stress analoga alla resistenza allo reologico causa appiattimento del campione. materiali fragili mostrano molto meglio capacità di resistere alla deformazione di compressione, piuttosto che deformazione dilatativa; per chi, la deformazione di rottura compressione supera il carico di rottura polivalente. Rottura di materiali fragili sotto compressione si verifica a causa di cracking.
disegno grafico è la stesso come nel caso della tensione. Sotto una deformazione di compressione, il campione si accorcia; Nel frattempo, le dimensioni della sezione trasversale crescono. Per alcuni materiali plastici, è impossibile trovare lo stress analoga alla resistenza allo reologico causa appiattimento del campione. materiali fragili mostrano molto meglio capacità di resistere alla deformazione di compressione, piuttosto che deformazione dilatativa; per chi, la deformazione di rottura compressione supera il carico di rottura polivalente. Rottura di materiali fragili sotto compressione si verifica a causa di cracking.
Volume sforzo-deformazione di Stato a un punto
Lo stato deformato in un punto di un corpo deformabile è descritto dal tensore di deformazione simmetrica:
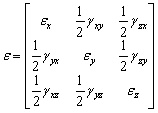 ,
,
dove ![]() - la deformazione longitudinale relativa,
- la deformazione longitudinale relativa, ![]() ,
, ![]() ,
, ![]() - la deformazione angolare. È sempre possibile specificare le tre direzioni ortogonali, in modo che gli angoli a picco sono tutti zeri, mentre allungamenti sono
- la deformazione angolare. È sempre possibile specificare le tre direzioni ortogonali, in modo che gli angoli a picco sono tutti zeri, mentre allungamenti sono ![]() . Le deformazioni
. Le deformazioni ![]() ,
, ![]() ,
, ![]() nelle direzioni, per cui angoli puri sono assenti, sono chiamati deformazioni principali in un punto.
nelle direzioni, per cui angoli puri sono assenti, sono chiamati deformazioni principali in un punto.
Insieme, i nove componenti della matrice dello stress, tre per ciascuna delle facce mutuamente perpendicolari, costituiscono un'entità fisica chiamata, tensore degli sforzi in un punto. Il tensore è rappresentata da una matrice simmetrica:
 ,
,
dove ![]() - la sollecitazione di compressione-tensione,
- la sollecitazione di compressione-tensione, ![]() ,
, ![]() ,
,![]() , - la tensione di taglio.
, - la tensione di taglio.
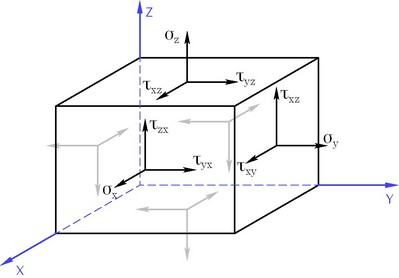
I componenti del tensore stato tensionale in un blocco di infinitesimo
La seguente regola dei segni è comunemente utilizzato per i componenti di stress tensoriali: un componente è positivo, se punta nella direzione positiva delle rispettive coordinate assi di una sfaccettatura con il positivo normale esterna allineata con una delle coordinate.
Sia il tensore degli sforzi e il tensore di deformazione possiedono la proprietà di simmetria. ![]() ,
, ![]() ,
,![]() . Le condizioni di simmetria del tensore degli sforzi sono anche denominati come sforzi di taglio appaiati: gli sforzi di taglio che agiscono su due facce reciprocamente perpendicolari nelle direzioni ortogonali al bordo nell'intersezione di questi aspetti sono uguali in ampiezza. Grazie a queste proprietà, su nove componenti del tensore di stress ci sono sei indipendenti.
. Le condizioni di simmetria del tensore degli sforzi sono anche denominati come sforzi di taglio appaiati: gli sforzi di taglio che agiscono su due facce reciprocamente perpendicolari nelle direzioni ortogonali al bordo nell'intersezione di questi aspetti sono uguali in ampiezza. Grazie a queste proprietà, su nove componenti del tensore di stress ci sono sei indipendenti.
Come nel caso del ceppo, il concetto di tensioni principali viene introdotto in uno stato di tensione, ![]() , corrispondenti ai ceppi principali, relativi alle componenti di stress tensore dall'equazione:
, corrispondenti ai ceppi principali, relativi alle componenti di stress tensore dall'equazione:
![]() , dove
, dove
![]() ,
,  ,
, 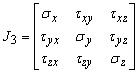
Una soluzione dell'equazione cubica ha tre radici reali ![]() , che sono comunemente ordinata come segue:
, che sono comunemente ordinata come segue: ![]() . Le tensioni principali possiedono una proprietà importante: le sollecitazioni normali sui principali aspetti di direzione orientata sono più alti tra quelli su altri aspetti. Anche introdotto è il concetto di stress media con la formula
. Le tensioni principali possiedono una proprietà importante: le sollecitazioni normali sui principali aspetti di direzione orientata sono più alti tra quelli su altri aspetti. Anche introdotto è il concetto di stress media con la formula
![]()
Strutture statiche Forza di valutazione. Teorie Forza
L'ultimo stato tensionale sicuro è quando le proprietà del materiale subiscono un cambiamento qualitativo - una transizione da uno stato meccanico ad un'altra. Per i materiali plastici, lo stato ceppo sicurezza è comunemente considerato come la condizione di sviluppare notevole deformazione residua, mentre per quelli fragili - una condizione in cui un materiale comincia a incrinarsi. Lo stato finale non è ammissibile per i materiali. Pertanto, durante l'esecuzione di analisi forza, perseguire l'cosiddetto stato ricevibile. Esso corrisponde al carico ottenuto dividendo il carico dello stato finale resistenza da un fattore di sicurezza. Se i fattori di sicurezza sono uguali in due stati di stress, quelli sono chiamati ugualmente fail-safe. Per confrontare i vari stati tesi, la semplice tensione (compressione) è accettato come la misura universale, con la sollecitazione principale ![]() .
.
Eollecitazione equivalente ![]() - lo stress da sviluppare in un campione allungate in modo da rendere il suo stato altrettanto pericoloso come uno stato di stress specificato. Il criterio di forza è scritto come
- lo stress da sviluppare in un campione allungate in modo da rendere il suo stato altrettanto pericoloso come uno stato di stress specificato. Il criterio di forza è scritto come ![]() .
.
teorie di forza sono le ipotesi circa i criteri che descrivono le condizioni di un materiale di raggiungere il massimo stato di forza.
Teoria della Prima Resistenza
Nella prima teoria resistenza, resistenza alla trazione di un materiale si riferisce alla sollecitazione massima normale. Secondo questa teoria, lo stato pericoloso si verifica quando una delle tensioni principali raggiunge una soglia di sicurezza. Pertanto, l'entità delle sollecitazioni massime principali è limitata in modo da non superare la sollecitazione massima principale ![]() . Il criterio di forza appare come:
. Il criterio di forza appare come: ![]() , dove
, dove ![]() , se
, se ![]() e
e ![]() , se
, se ![]() .
.
Teoria della Seconda Resistenza
La seconda teoria forza usa la massima deformazione come l'ultimo criterio di forza. Secondo questa teoria, lo stato non sicuro di un materiale verifica quando deformazione lineare raggiunge una certa soglia di sicurezza. Per un materiale plastico, il criterio di resistenza appare come ![]() , dove
, dove ![]() . Se, per esempio,
. Se, per esempio, ![]() , allora
, allora ![]() .
.
Per i materiali fragili, il criterio di forza appare come:
![]() ,
, ![]()
La prima teoria produce un buon accordo con i dati sperimentali solo per materiali fragili. Il secondo è praticamente abbandonato al giorno d'oggi.
Teoria della Terza Resistenza
Nella terza teoria forza, la resistenza alla trazione si riferisce alla sollecitazione massima pura. Secondo questa teoria, lo stato pericoloso si verifica quando la massima tensione tangenziale raggiunge una soglia di sicurezza.
Il criterio di forza appare come: ![]() , dove
, dove ![]() . Di conseguenza:
. Di conseguenza: ![]()
Quarto teoria forza (energia)
La quarta teoria forza è basata sull'approccio energetico, basata sull'ipotesi che la causa di uno stato non sicuro è la grandezza del potenziale densità di energia di deformazione uф, quindi il criterio si riferisce alla densità dell'energia potenziale di deformazione.
Vi derivare la formula per il potenziale densità di energia dovuta alla distorsione dalla formula per l'intero potenziale densità di energia dovuta alla deformazione, utilizzando il rapporto specifico di Poisson di µ =0.5.
Che produce:
![]()
Il criterio di forza appare come ![]() , dove
, dove ![]() .
.
Di conseguenza:
![]()
oppure
![]()
La terza e la quarta teoria di resistenza producono un accordo soddisfacente trai risultati teorici di calcolo con i dati di test di laboratorio per materie plastiche e sono ampiamente utilizzati nell'analisi della forza. Queste teorie non sono applicabili per materiali fragili.