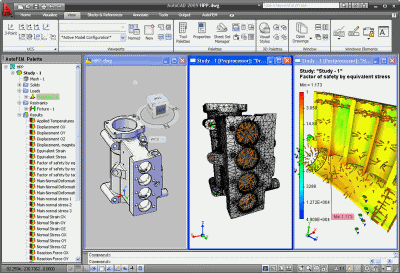
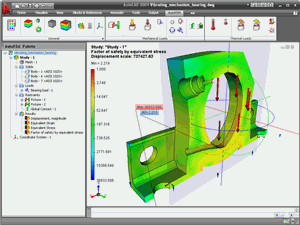
AutoFEM Analysis is the finite element analysis software.
The main feature of the system is its deep integration with AutoCAD

Using AutoFEM Analysis, an AutoCAD user gets a possibility to solve the problem of finite-element modeling of various physical phenomena:

• Static analysis (analysis of structural stress and strain) - the AutoFEM Static Analysis module;
• Stress analysis for structures under cyclic loading action - the AutoFEM Fatigue Analysis module;
• Calculation of natural frequencies (resonances) of structures - the AutoFEM Frequency Analysis module;
• Calculation of critical load (the system's stability) - the AutoFEM Buckling Analysis module;
• Calculations of temperature (or distribution of temperature domains) - the AutoFEM Thermal Analysis module .

The general algorithm of working with AutoFEM Analysis is as follows:

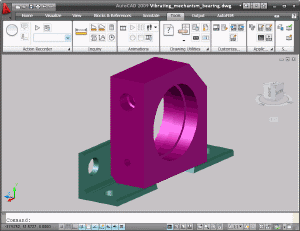
First, the user should create a three-dimensional (3D) model of the product in the AutoCAD 3D environment.

Then, without leaving AutoCAD, the user should create the problem of finite element analysis, referred to as the “Study”.
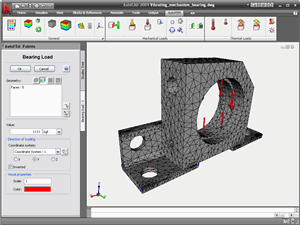
The model is loaded into an AutoFEM Analysis pre-processor integrated into AutoCAD.

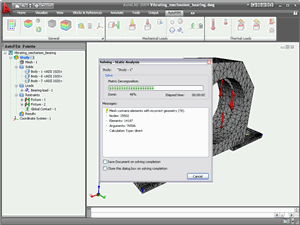
Using the pre-processor, the user specifies external and internal parameters of simulated physical phenomena (finite element mesh, boundary conditions, materials, etc.) and transmits the “Study” to an AutoFEM Analysis processor.

The AutoFEM Analysis processor creates and solves systems of algebraic equations in accordance with the finite element method. With the help of an AutoFEM Analysis post-processor, the user performs analysis of results and develops the accompanying documents, i.e. reports, video, avi, etc.

Users of AutoCAD become able to perform the finite element analysis in the usual and familiar software environment.
There is the FREE finite element analysis software - AutoFEM Analysis Lite - which is available for use to each user of AutoCAD 2007-2010.

Theoretical background of AutoFEM Analysis

AutoFEM Analysis – is the finite element analysis software, based on the finite element method.

The Finite element method (FEM) is the leading way of predicting the behavior of structures under real-life conditions.
The general principle of the finite element method is as follows.

The design, which is, generally speaking, a system with an infinite number of degrees of freedom, is divided into a finite number of elementary volumes, or the so-called finite elements. Since the form of the finite element is known in advance (bar, beam, triangle, wedge, prism, etc.), it is possible to write down the relations that establish a mathematical relationship between variations of a physical quantity within single element.

For example, in the problem of static stress analysis, the dependence of a geometric shape of the finite element (strain) is determined for the element influenced by external forces. The geometric shape of the finite element is defined by spatial coordinates of points on its boundaries that are called nodes. Application of forces to finite elements causes a shift of nodes (the strain). This shift can be expressed in the form of algebraic equations. In case of thermal analysis, regularities of temperature distribution in terms of finite elements are determined.

For each finite element, the system of algebraic equations is constructed as a mathematical formulation of the physical problem. For instance, for the problem related to static strength, the system of equations can be written in a matrix form:

[K^el] * [X^el] = [P^el], where

[K^el] - means the stiffness matrix of finite element
[P^el] - means the vector of forces applied to the finite element; and
[X^el] - means - an unknown vector of displacement at topical points of the finite element, called nodes. It is this vector which is to be determined.

In the first version AutoFEM Analysis as a finite element used tetrahedron. Tetrahedron can approximate arbitrarily complex geometry of the simulated real object. A special generator of finite element mesh creates a tetrahedral finite element mesh for three-dimensional solid model of a product, made in AutoCAD.

After building the finite element mesh and the computation of local stiffness matrices of each finite element it is possible to algebraically and topologically sum up all the local stiffness matrix elements and to construct the global stiffness matrix of the assembly. The result (for example, stress static analysis) is a system of equations of the form

[K^Gl] * [X^GL] = [P^Gl], where

[K^Gl] - global stiffness matrix of construction.
[P^Gl] - the global vector of external forces.
[X^G] - to be determined the vector of unknown nodal displacements.

Processor of AutoFEM Analysis performs the generation of the global stiffness matrix and solution of algebraic equations. There are some methods for solving algebraic equations. One of the most famous and used is Gauss method (or its modifications such as Cholesky method). These methods usually are called as Direct methods of algebraic equations solving. The second big group of linear algebra methods for solving algebraic equations is Iterative methods of algebraic equations solving such as Conjugate gradient method.

Processor of AutoFEM Analysis uses both of these groups methods for solvinglinear and non-linear algebraic equations which are considered in finite element modeling.

After solving the equations at each node of the finite element mesh is known displacement and stress (for statics), or other physical quantities such as temperature for the thermal analysis. These data are transmitted into Postprocessor of AutoFEM Analysis, which has been fully integrated into the interface of AutoCAD.

The theory of finite element method is described in many books and articles. It is not easy to recommend any of them, because there quantities is about hundred of thousands. Possibly one of the most famous author about FEM theme is O.C. Zienkiewicz. His books have been translated into all European languages. For example, one of the last edition of his book is Zienkiewicz O.C., Taylor R.L. Vol. 1-3. The finite element method. (2000)(T).

AutoFEM Analysis uses various finite element algorithms which are described in scientific articles and special books on FEA and FEM thematic.