Language

AutoFEM Analysis ist ein System der Finite-Elemente-Analyse.
Das wichtigste Merkmal des Systems ist seine tiefe Integration in AutoCAD.

AutoFEM Analysis ist ein System von Finite-Elemente-Analyse.

Mit AutoFEM Analysis hat der AutoCAD-Anwender die Fähigkeit, Probleme der Finite-Element-Modellierung von verschiedenen physikalischen Phänomenen zu lösen:

Der Generelle Algorithmus von AutoFEM ist der folgende:
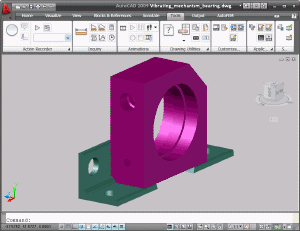
Zuerst erstellt der Benutzer ein dreidimensionales (3D) Modell des gewünschten Produkts in der Umgebung von AutoCAD.

Dann, ohne AutoCAD zu verlassen, erstellt der Benutzer ein Problem der Finite-Elemente-Analyse, die sogenannte «Studie». Das Modell wird in den Vorprozessor AutoFEM geladen, welcher in AutoCAD integriert ist.

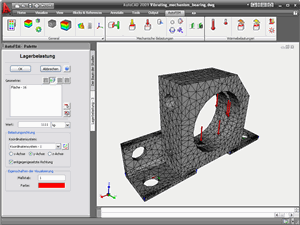
Mit dem Vorprozessor legt der Benutzer die externen und internen Parameter der Simulation physikalischer Phänomene (Finite-Elemente-Netz, Randbedingungen, Materialien, etc.) fest und überträgt sie der "Prüfung" im Prozessor AutoFEM.

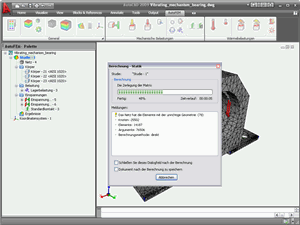
Der Prozessor AutoFEM führt die Berechnung von Systemen in algebraischen Gleichungen mit der Finite-Elemente-Methode durch.

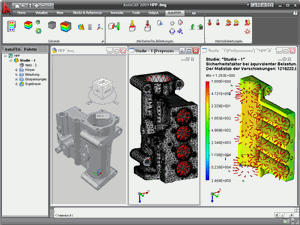
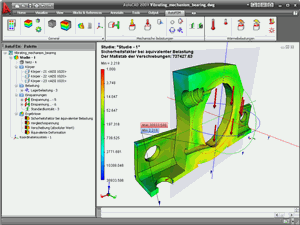
Im folgenden Postprozessor AutoFEM führt der Benutzer eine Analyse der Ergebnisse durch und kann die zugehörigen Unterlagen erstellen - Berichte, .avi Videos, etc.
Mit AutoFEM haben AutoCAD-Anwender also die Möglichkeit Finite-Elemente-Simulationen in der gewohnten und vertrauten der Software-Umgebung durchzuführen.

Download Demo-Video über AutoFEM Statische Analyse

Theoretischer Hintergrund der Analyse AutoFEM

AutoFEM Analysis ist eine Finite-Elemente-Analyse-Software, basierend auf der Finite-Elemente-Methode. Die Finite Elemente Methode (FEM)

ist der führende Weg das Verhalten von Strukturen in realen Bedingungen vorherzusagen.
Das allgemeine Prinzip der Methode der finiten Elemente ist der folgende:
Das Design, das im Allgemeinen ein System mit einer unendlichen Anzahl von Freiheitsgraden ist, wird in eine endliche Anzahl von elementaren Strukturen, die so genannte Finite-Elemente, unterteilt. Da die Form eines Finite-Elements im Voraus bekannt ist (Stab, Dreieck, Kasten, etc.) ist es möglich, die Beziehungenund den mathematischen Zusammenhang einer physikalischen Größe in einem einzelnen Element zu berechnen.
Zum Beispiel ist für das Problem der statischen Festigkeitsanalyse die Abhängigkeit der geometrischen Form des Finite-Elements(Stamm) durch die äußeren Kräfte bestimmt. Diegeometrische Form eines Finite-Elements wird durch die räumlichen Koordinaten bestimmter Punkte auf die Grenzen des Finite-Elements definiert, die Knoten (nodes) genannt werden. Eine Anwendung von Kraft auf die Finite-Elemente bewirkt eine Verschiebung der Knoten (Stamm). Diese Verschiebung kann in Form von algebraischen Gleichungen ausgedrückt werden. Für die thermische Analyse werden die Gesetze der Temperaturverteilung auf die Finite-Element angewandt.
Für jedes Finite Element beschreibt ein System von algebraischen Gleichungen das physikalische Problem. Zum Beispiel kann für das Problem der statischen Festigkeit in der Form einer Matrix das System von Gleichungen so beschrieben werden:

[Kel] * [Xel] = [Pel], wo

[Kel] - Steifigkeitsmatrix der Finite-Elemente.
[Pel] - Vektor der Kräfte, die auf der Finite-Elemente wirkt.
[Xel] - der unbekannte Vektor der Verschiebungen an charakteristischen Punkten der Finite-Elemente, die als Knoten bezeichnet werden. Dieser Vektor soll bestimmt werden.
In der ersten Version der AutoFEM Analysis wurden Tetraeder als Finite-Elemente verwendet. Tetraeder können annähernd beliebig komplexe Geometrien von realen Objekten simulieren- Ein spezieller Finite-Elemente-Generator stellt ein tetraedrisches Finite-Elemente-Gitter für das dreidimensionale Volumenmodell des realen Produktes welches in AutoCAD gemacht wurde.
Nach dem Bau des Finite-Elemente-Netzes und der Berechnung der lokalen Steifigkeitsmatrizen jedes Finite-Elementes ist es möglich, algebraisch und topologisch die Summe aller lokalen Steifigkeitsmatrizen zu einer globalen Steifigkeitsmatrix zu vereinen. Das Ergebnis (z. B. statische Analyse) ist ein System von Gleichungen der Form

[KGL] * [XGL] = [PGL], wo

[KGL] - globale Steifigkeitsmatrix der Konstruktion.
[PGL] - Die globale Vektor der äußeren Kräfte.
[XGL] - Dieunbekannten Knotenverschiebungen, die bestimmt werden müssen. Der Prozessor der AutoFEM Analyse führt die Generation der globalen Steifigkeitsmatrix und Lösung der algebraischen Gleichungen an. Es gibt mehrere Methoden zur Lösung von algebraischen Gleichungen. Eine der berühmtesten die verwendet wird ist das Gauß-Verfahren (oder dessen Modifikationen das Cholesky-Verfahren). Diese Methoden sind in der Regel als direkte Methoden algebraische Gleichungen zu lösen bekannt. Die zweite große Gruppe der linearen Algebra-Methoden zur Lösung von algebraischen Gleichungen sind Iterative Methoden algebraischen Gleichungen zu lösen, wie zum Beispiel das CG-Verfahren.

Der Prozessor der AutoFEM Analysis verwendet diese beiden Gruppen von Methoden zur Lösung von linearen und nicht-linearen algebraischen Gleichungen, die in Finite-Element-Modellierung vorkommen.Nach der Lösung der Gleichungen an jedem Knoten des Finite-Elemente-Netzes ist die Verschiebung und der Stress (Statik), oder andere physikalische Größen wie Temperatur für die thermische Analyse bekannt. Diese Daten werden in den Postprozessor AutoFEM Analysis übertragen, der vollständig in die Benutzeroberfläche von AutoCAD integriert ist.Die Theorie der Finite-Elemente-Methode wird in vielen Bücher und Artikel beschrieben. Es ist nicht leicht, einen von ihnen empfehlen, denn es geht mengenmässig in die Hunderttausende. Möglicherweise einer der berühmtesten Autoren zum Thema FEM ist O.C. Zienkiewicz.

Seine Bücher wurden in alle europäischen Sprachen übersetzt. Zum Beispiel ist eine der letzten Auflage seines Buches empfehlenswert: Zienkiewicz OC, RL Taylor Vol. 1-3. Die Methode der finiten Elemente. (2000) (T).
AutoFEM Analysis verwendet verschiedene Finite-Elemente-Algorithmen, die in wissenschaftlichen Artikeln und Bücher über FEA und FEM-Thematiken beschrieben werden.